Пример решения задачи ЛП с двумя переменными
Графическим методом
Пример №2.1.
Найти оптимальное решение примера №1.2 о производстве мыла, математическая модель которой имеет вид
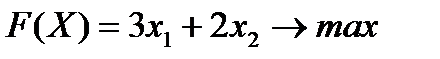
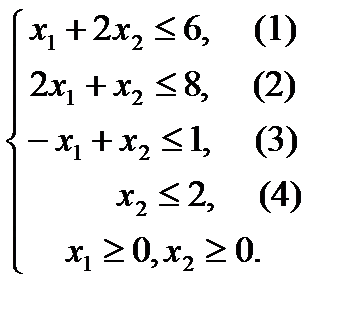
Решение.
Для построения прямых ограничений необходимо вычислить координаты точек пересечения этих прямых с осями координат (рис.2.2).
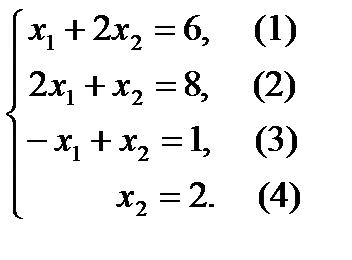
(1) – 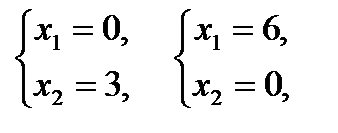 (2) –
(2) – 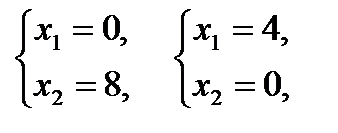
(3) – 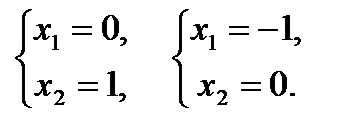
Прямая (4) проходит через точку x2 =2 параллельно оси x1.

Рис. 2.2. Графическое решение
Далее следует определить область допустимых значений. Например, подставив точку (0;0) в исходное ограничение (3), результатом является неравенство  , что является истинным. Поэтому стрелкой (или штрихованием) обозначается полуплоскость, содержащая точку (0;0), т.е. расположенная правее и ниже прямой (3). Аналогично определяются допустимые полуплоскости для остальных ограничений (рис.2.2). Общей областью, разрешенной всеми ограничениями, т.е. областью допустимых значений является многоугольник ABCDEF.
, что является истинным. Поэтому стрелкой (или штрихованием) обозначается полуплоскость, содержащая точку (0;0), т.е. расположенная правее и ниже прямой (3). Аналогично определяются допустимые полуплоскости для остальных ограничений (рис.2.2). Общей областью, разрешенной всеми ограничениями, т.е. областью допустимых значений является многоугольник ABCDEF.
Целевую прямую можно построить по уравнению
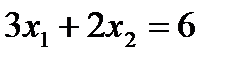 ,
,
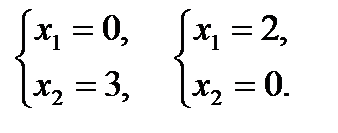
Вектор  строится из точки (0;0) и направляется в точку (3;2). Точка Е – это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлению вектора
строится из точки (0;0) и направляется в точку (3;2). Точка Е – это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлению вектора  . Поэтому Е – это точка максимума целевой функции. Координаты точки Е определяются из системы уравнений прямых ограничений (1) и (2)
. Поэтому Е – это точка максимума целевой функции. Координаты точки Е определяются из системы уравнений прямых ограничений (1) и (2)
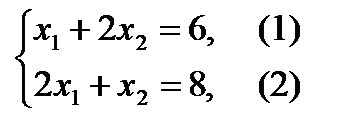
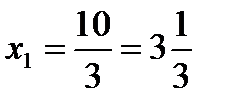 ,
, 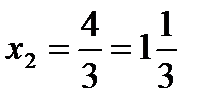 ,
,
Е( 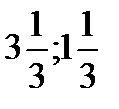 ) [т/сутки].
) [т/сутки].
Максимальное значение целевой функции равно
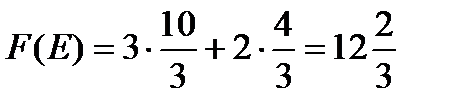 [тыс. руб./сутки].
[тыс. руб./сутки].
Ответ.
Наилучшим режимом работы фабрики является ежесуточное производство хозяйственного мыла в объеме 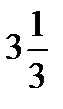 т и туалетного мыла в объеме
т и туалетного мыла в объеме  т.
т.
Доход от продажи мыла составит 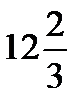 тыс. руб. в сутки.
тыс. руб. в сутки.
Дата добавления: 2016-04-02; просмотров: 1176;
