Алгоритм симплексного метода
Шаг 1. Привести систему ограничений и функцию цели к каноническому виду. Составить матрицу условий-ограничений.
Шаг 2. Определить допустимое решение задачи ЛП и вычислить значение целевой функции.
Шаг 3.Составить первую симплексную таблицу.
Шаг 4.Проверить симплексную таблицу на оптимальность.
Шаг 5. Если симплексная таблица оптимальная, то вычисления прекратить. Если нет, то симплексную таблицу необходимо пересчитать по соответствующему алгоритму и составить новую симплексную таблицу.
Шаг 6. Если новая симплексная таблица не содержит оптимального решения, то ее тоже необходимо пересчитать. Пересчет повторять до тех пор, пока не будет найдено оптимальное решение.
Пусть имеется задача ЛП, в системе ограничений которой не содержится неравенств.
Минимизировать или максимизировать
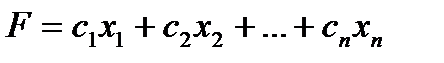(3.1)
при условиях
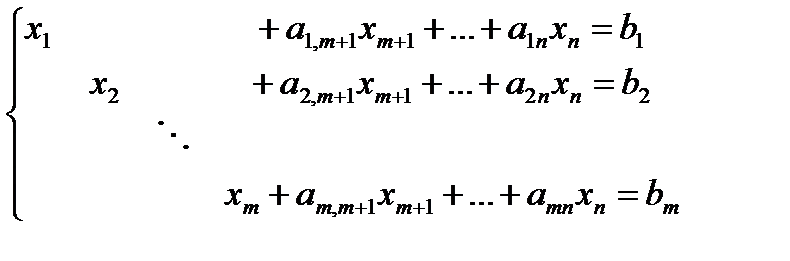(3.2)
, 
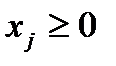(3.3)
Шаг 1.
В системе ограничений задачи не содержится неравенств.
Для составления матрицы системы ограничений необходимо выписать все коэффициенты системы (3.2) в виде матрицы:
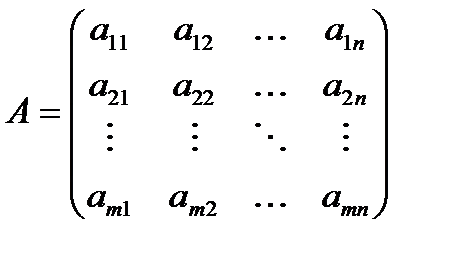(3.4)
Для удобства решения исходные данные задачи лучше представить в виде матриц значений:
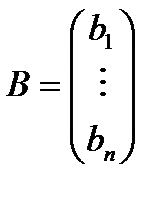
Шаг 2.
Одним из допустимых решений задачи ЛП (3.1) – (3.3) будет базисное неотрицательное решение системы (3.2):
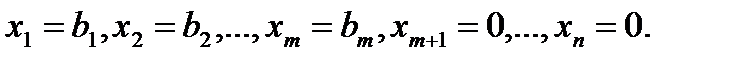(3.5)
т.к. предполагается, что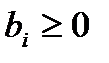 
, i=1,2,…,m.
Ему соответствует значение целевой функции, равное
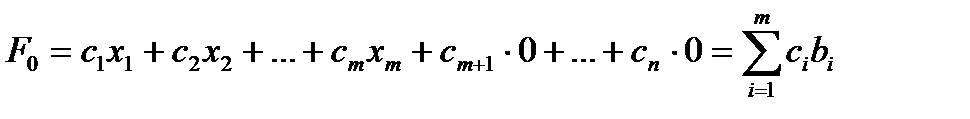. (3.6)
Шаг 3.
Симплексная таблица представляет собой таблицу следующего вида:
Таблица 3.1. – Симплексная таблица
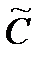
| Базис | B | с1 | с2 | … | сm | сm+1 | … | сj | … | сn |
| x1 | x2 | … | xm | xm+1 | … | xj | … | xn | |||
| с1 | x1 | b1 | … | a1,m+1 | … | a1,j | … | a1,n | |||
| с2 | x2 | b2 | … | a2,m+1 | … | a2,j | … | a2,n | |||
| … | … | … | … | … | … | … | … | … | … | … | … |
| сm | xm | bm | … | am,m+1 | … | am,j | … | am,n | |||
| F0-F | … |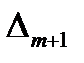 
| … | 
| … | 
|
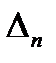
Основу первой симплексной таблицы составляет матрица системы ограничений (3.4).
В верхней строке данной таблицы вписываются все коэффициенты С линейной формы (3.1).
В первые два столбика заносятся коэффициенты при базисных неизвестных из целевой функции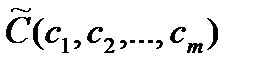 
и сами базисные неизвестные.
В третий столбец заносятся свободные члены системы ограничений.
В последней строке записываются коэффициенты при неизвестных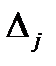 
и свободный член уравнения F0.
Коэффициенты 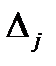определяются по формуле:
(3.7)
zj – сумма построчных произведений коэффициентов j-го столбца (j-й переменной) на коэффициенты при соответствующих базисных переменных (в симплексной таблице записываются в первом столбце)
, 
;
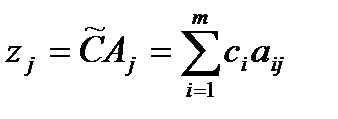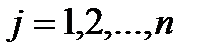или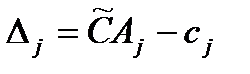 
, где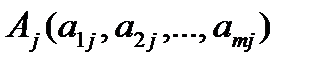 
.
Шаг 4.
Для проверки симплексной таблицы на оптимальность необходимо знать следующие правила оптимальности при поиске минимума и максимума функции.
Правила оптимальности для минимизации функции
Правило №1.
Если все коэффициентов 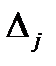, стоящие в последней строке симплексной таблицы по столбцам свободных неизвестных меньше нуля, то найдено оптимальное решение задачи ЛП. Функция цели достигает минимума на множестве допустимых решений, т. е. условие оптимальности имеет вид
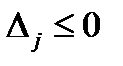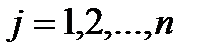, . (3.8)
Правило №2.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент 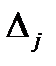при ней в последней строке симплексной таблицы положителен и в этом же столбце симплексной таблицы нет ни одного положительного коэффициента, то задача ЛП неразрешима.
Правило №3.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент 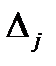при ней в последней строке симплексной таблицы положителен и в этом же столбце симплексной таблицы есть хотя бы один положительный коэффициент, то существует оптимальное решение задачи ЛП, для нахождения которого необходимо пересчитать симплексную таблицу по соответствующему алгоритму.
Правила оптимальности для максимизации функции
Правило №1.
Если все коэффициентов 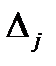, стоящие в последней строке симплексной таблицы по столбцам свободных неизвестных больше нуля, то найдено оптимальное решение задачи ЛП. Функция цели достигает максимума на множестве допустимых решений, т. е. условие оптимальности имеет вид
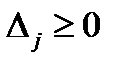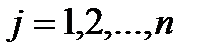, . (3.9)
Правило №2.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент 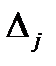при ней в последней строке симплексной таблицы отрицателен и в этом же столбце симплексной таблицы нет ни одного положительного коэффициента, то задача ЛП неразрешима.
Правило №3.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент 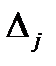при ней в последней строке симплексной таблицы отрицателен и в этом же столбце симплексной таблицы есть хотя бы один положительный коэффициент, то существует оптимальное решение задачи ЛП, для нахождения которого необходимо пересчитать симплексную таблицу по соответствующему алгоритму.
Первую симплексную таблицу еще называют базисным планом.
Шаг 5.
Если не найдено оптимальное решение и выполняется правило №3, то необходимо первую симплексную таблицу пересчитать по соответствующему алгоритму.
Дата добавления: 2016-04-02; просмотров: 864;