ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ

Задача планирования производства состоит в отыскании такого плана 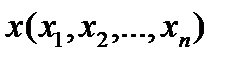, который позволяет получить максимальную прибыль

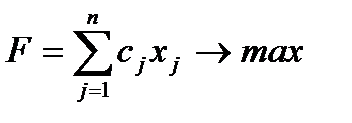(4.1)

при ограничениях по заданным ресурсам

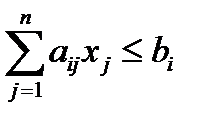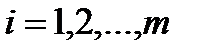, (4.2)

где по смыслу задачи

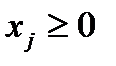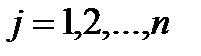, . (4.3)

При этом по оптимальному плану производства некоторые ресурсы используются полностью (дефицитные), а другие ресурсы избыточны.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями (матрицей условий A), со структурой и количеством ресурсов (вектором B), а также со структурой внешних цен (вектор прибылей C). Эти оценки называются расчетными оценками ресурсов.

Пусть имеется другое предприятие – кооператив, который может использовать все имеющиеся у первого предприятия различные виды сырья для выпуска совершенно других изделий по своим технологиям и ставит вопрос о том, чтобы предприятие «уступило» кооперативу имеющееся у них сырье по «договорным» ценам. Как установить эти цены?

Пусть

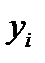– оценка единицы i-го вида ресурса;

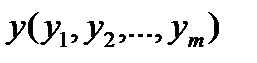– вектор оценок ресурсов;

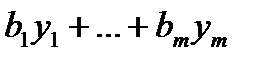– суммарная оценка всех ресурсов представится.

Естественно, эту сумму кооператоры стремятся минимизировать путем изменения оценок 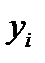. Со своей стороны предприятие должно учесть, что на производство единицы продукции j-го вида оно должно затратить различные виды ресурсов в количествах 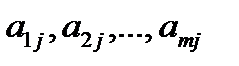и их суммарная оценка будет равна . Очевидно, что имеет смысл «уступить» кооператорам только в том случае, если эта сумма будет не меньше той прибыли, которую получит предприятие от реализации единицы готового изделия.

Таким образом, формулируется новая задача ЛП:

найти вектор оценок ресурсов 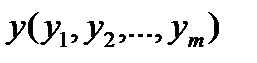, минимизирующий суммарную оценку всех ресурсов

(4.4)

при условиях

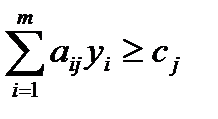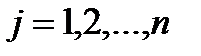, , (4.5)

где по смыслу задачи 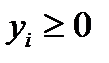, 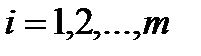. (4.6)

Полученная задача ЛП (4.4) – (4.6) называется двойственной задачей к задаче (4.1) – (4.3). Расчетные оценки ресурсов, соответствующие оптимальному плану производства, служат компонентами оптимального решения двойственной задачи. Поэтому компонента 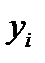оптимального решения двойственной задачи называется двойственной оценкой i-го ресурса.

Задачи (4.1) – (4.3) и (4.4) – (4.6) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видно, что двойственная задача составляется согласно следующим правилам.