КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА
В настоящее время задачи транспортного типа или задача прикрепления поставщиков к потребителям стала типовой для промышленных предприятий, имеющих в своем составе несколько фирм, складов, оптовых баз и рынков сбыта. Эти задачи применяются для выбора оптимальных маршрутов доставки продукции от поставщиков к потребителям.
Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции, производимой (хранимой) в нескольких пунктах производства (хранения).
В общем виде задача может быть сформулирована следующим образом.
Однородный продукт, сосредоточенный в 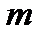 пунктах производства (хранения) в количествах
пунктах производства (хранения) в количествах 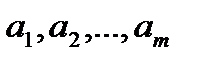 единиц, необходимо распределить между
единиц, необходимо распределить между 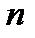 пунктами потребления, которым необходимо соответственно
пунктами потребления, которым необходимо соответственно 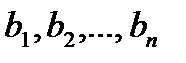 единиц. Стоимость перевозки единицы продукции из i-го пункта отправления в j-й пункт назначения равна cij и известна для всех маршрутов. Необходимо составить план перевозок, при котором:
единиц. Стоимость перевозки единицы продукции из i-го пункта отправления в j-й пункт назначения равна cij и известна для всех маршрутов. Необходимо составить план перевозок, при котором:
1) запасы всех поставщиков были реализованы;
2) спросы всех потребителей были удовлетворены;
3) суммарные затраты на перевозку были бы минимальными.
Если производство и потребление сбалансированы, т. е. суммарные запасы продукта у поставщиков равны суммарным запросам потребителей:
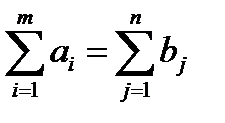 , (5.1)
, (5.1)
то такая транспортная задача называется закрытойили замкнутой. Если же суммарные запасы продукта у поставщиков строго больше или строго меньше, чем суммарные запросы потребителей, то такая задача называется открытой.
Для сведения открытой задачи к закрытой вводятся фиктивные пункты производства или потребления. Если суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, вводится фиктивный потребитель, запросы которого равны 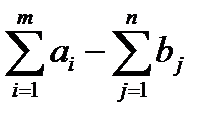 . Если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится фиктивный поставщик, запас продукта у которого равен
. Если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится фиктивный поставщик, запас продукта у которого равен 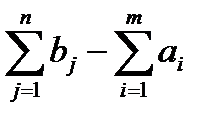 .
.
План перевозок, содержащий фиктивные поставки, называется вырожденным.
Пусть
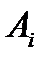 – пункты производства некоторой однородной продукции,
– пункты производства некоторой однородной продукции,  ;
;
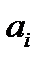 – объем производства в пункте
– объем производства в пункте 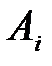 ;
;
 – пункты потребления продукции,
– пункты потребления продукции,  ;
;
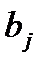 – потребность в продукции пункта
– потребность в продукции пункта  ;
;
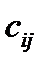 – стоимость перевозки единицы продукции из пункта
– стоимость перевозки единицы продукции из пункта 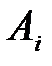 в любой пункт
в любой пункт  .
.
| А1 |
| А2 |
| Аm |
| B1 |
| B2 |
| Bn |
| с11 |
| с12 |
| с2n |
| сmn |
| с22 |
| сm1 |
| а1 |
| а2 |
| аm |
| b1 |
| b2 |
| bn |
| с1n |
Рис. 5.1. Транспортная задача
Дата добавления: 2016-04-02; просмотров: 1034;
