Математическая модель распределительной задачи
Найти минимум функции с учетом системы ограничений:
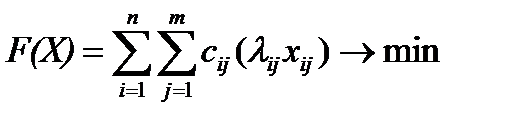
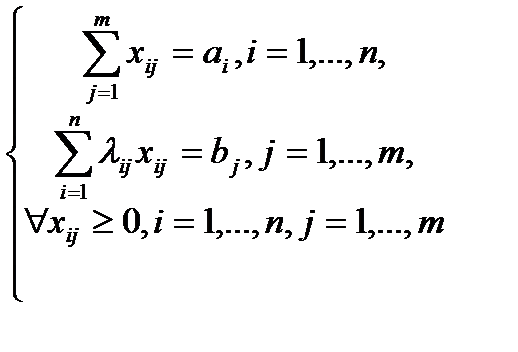(6.1)
где ( 
) – это количество работ j-го вида, выполненных i-м исполнителем.
Алгоритм решения распределительной задачи
Шаг 1. Преобразовать распределительную задачу в транспортную:
1)выбрать базовый ресурс и рассчитать нормированные производительности ресурсов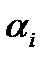 
:
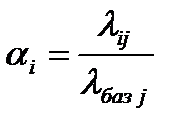(6.2)
2)пересчитать запаса рабочего ресурса исполнителей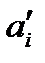 
:
(ед.ресурса); (6.3)
3)перерасчитать планового задания 
:
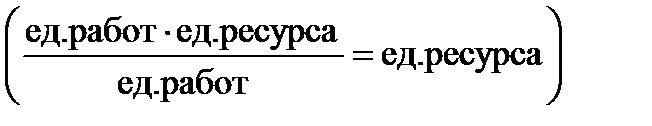; (6.4)
4)пересчитать себестоимости работ:
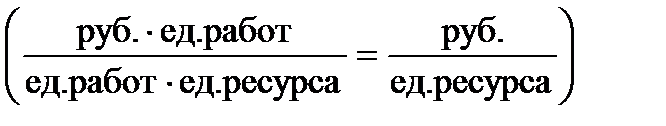. (6.5)
Шаг 2. Проверить баланспересчитанных параметров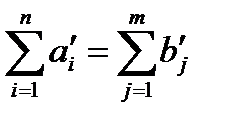 
.
Построить транспортную матрицу.
Шаг 3. Найти оптимальное решение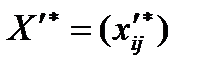 
.
Шаг 4. Преобразовать оптимальное решение транспортной задачи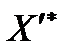 
в оптимальное решение распределительной задачи 
, причем переход 
выполняется по формуле:
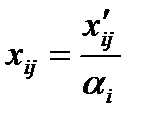(ед.ресурса), (6.6)
где xij и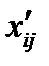 
– соответственно элементы решения распределительной и транспортной задач.
Шаг 5. Определить количество работ 
, соответствующее оптимальному решению распределительной задачи :
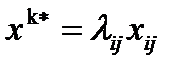
. (6.7)
Шаг 6. Определить целевую функцию распределительной задачи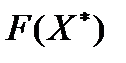 
согласно (6.1).
Дата добавления: 2016-04-02; просмотров: 1098;