Алгоритм решения транспортной задачи

Шаг 1. Привести открытую модель транспортной задачи к закрытой.

Шаг 2. Определить первое допустимое решение по правилу «северо-западного угла».

Правило северо-западного угла.

Заполнение транспортной таблицы начинается с левой верхней клетки («северо-западного угла») и состоит из однотипных шагов, на каждом из которых из рассмотрения исключается один поставщик или один потребитель:

1) если остаток продукта у i-го поставщика после предыдущих шагов меньше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения i-й поставщик, и в клетку (i, j) заносится поставка x_ij, равная остатку продукта у i-го поставщика после предыдущих шагов;

2) если остаток продукта у i-го поставщика после предыдущих шагов больше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения j-й потребитель, и в клетку (i, j) заносится поставка x_ij, равная неудовлетворенному запросу j-го потребителя;

3) если остаток продукта у i-го поставщика после предыдущих шагов равен неудовлетворенному запросу j-го потребителя, то исключается из рассмотрения или i-й поставщик, или j-й потребитель, и в клетку (i, j) заносится поставка x_ij, равная остатку продукта у i-го поставщика после предыдущих шагов. В случае исключения i-го поставщика в клетку (i+1, j) заносится поставка x_i+1,j = 0 равная неудовлетворенному запросу j-го потребителя. В случае исключения j-го потребителяв клетку (i, j+1) заносится поставка x_i,j+1= 0 равная остатку продукта у i-го поставщика после предыдущих шагов.

Шаг 3. Вычислить потенциалы.

1. Каждому поставщику ставится в соответствие потенциал p_i.

2. Каждому потребителю — потенциал q_j.

При этом каждой клетке соответствует некоторая оценка

, (5.6)

где ;

Один из потенциалов можно выбирать произвольно, т.к. в системе (5.3) и (5.4) одно уравнение линейно зависит от остальных. Обычно полагают p₁=0. Остальные потенциалы вычисляются из того условия, что для базисных клеток Δ_ij=0.

Шаг 4. Вычислить оценки всех свободных клеток по формуле (5.6).

Шаг 5. Проверить транспортнцю таблицу на оптимальность:

если среди оценок свободных клеток нет ни одной положительной, то базисное допустимое решение, содержащееся в данной транспортной таблице, является оптимальным.

Шаг 6. Если первая транспортная таблица оптимальная, то вычисления прекраить. Если нет, то транспортную таблицу необходимо пересчитать по соответствующему алгоритму и заполнить новую транспортную таблицу, вычислить новые потенциалы, оценки клеток и т.д.

Шаг 7. Процесс продолжать до тех пор, пока не будет получена транспортная таблица (и соответствующий план перевозок), для которой все

, ; .

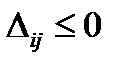Соответствующее последней транспортной таблице базисное решение является оптимальным.