Пример составления двойственной задачи

Пример №4.1.

Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции

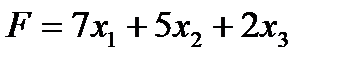(1)

при условиях

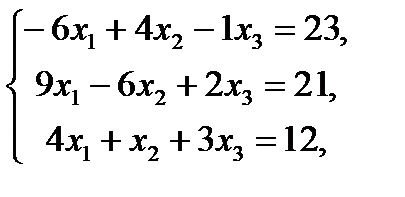(2)

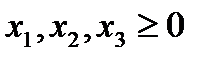(3)

Решение.

Для данной задач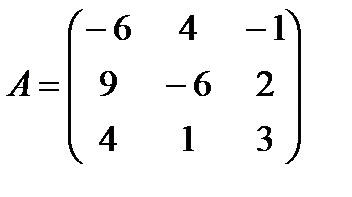и

и .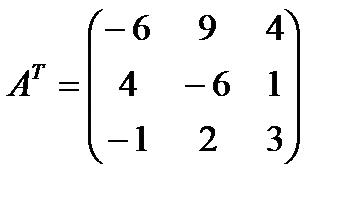

Число переменных в двойственной задаче равно числу уравнений в системе (2), т.е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (2), т.е. числа 23, 21, 12.

Целевая функция исходной задачи (1) – (3) исследуется на максимум, а система условий (2) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Т.к. все три переменные исходной задачи (1) – (3) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “ ”.

Ответ.

Для задачи (1) – (3) двойственная задача имеет вид:

найти минимум функции при условиях

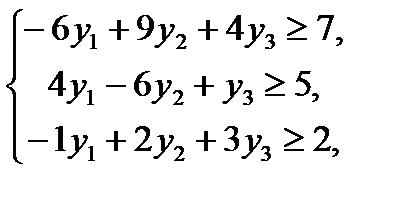
где у₁, у₂, у₃ – любого знака.

Пример №4.2.

Построить двойственную задачу к следующей задаче ЛП:

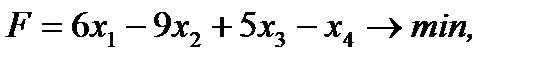
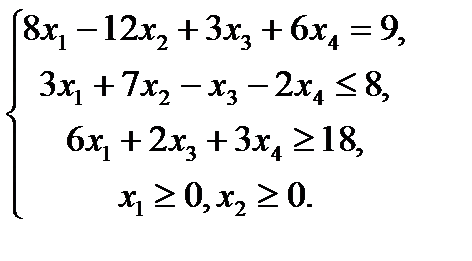
Решение.

Т.к. целевая функция минимизируется, то неравенства должны быть записаны с помощью знака ≥. Поэтому, прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной, умножив второе неравенство на (-1):

.

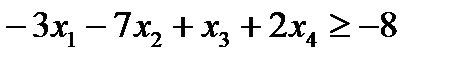Теперь, вводя двойственные переменные y₁, y₂, y₃ можно записать в соответствии с указанными правилами пару двойственных задач:

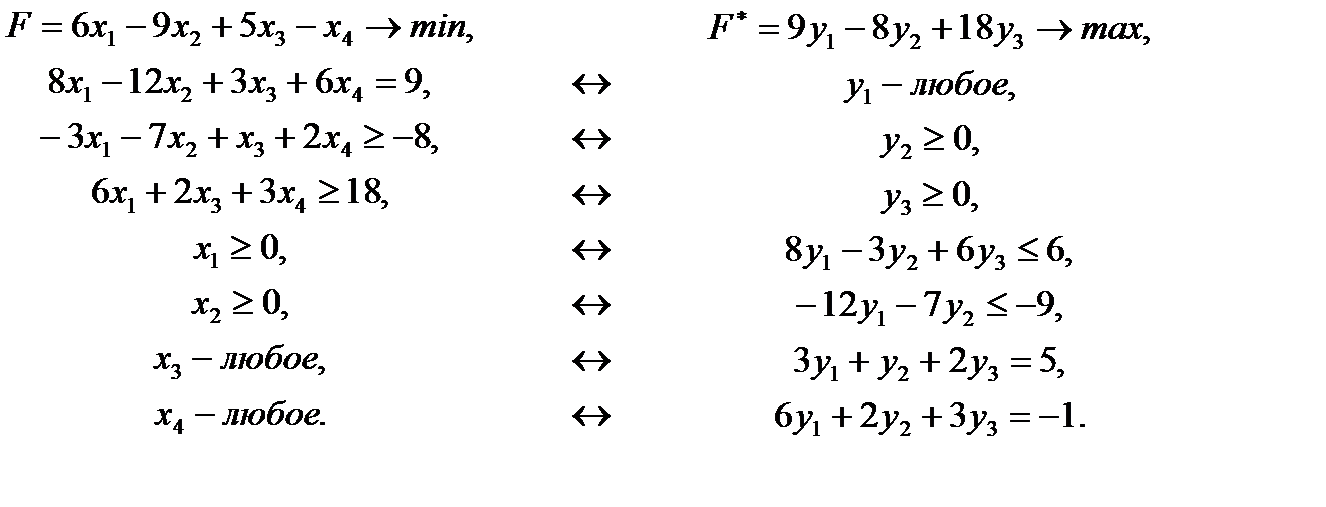
Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.

Каждая из задач двойственной пары фактически являтся самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методов оптимального плана одной из задач тем самым находится решение и другой задачи.

Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.

Лемма 1.

Если X – некоторый план исходной задачи, а Y – произвольный план двойственной задачи, то значение целевой функции исходной задачи при плане X всегда не превосходит значения целевой функции двойственной задачи при плане Y, т.е. .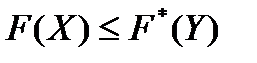

Лемма 2.

Если 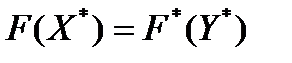для некоторых планов X^* и Y^* прямой и двойственной задач, то X^* – оптимальный план произвольный исходной задачи, а Y^* – оптимальный план двойственной задачи.