Правила составления двойственной задачи
1. Целевая функция исходной задачи (4.1) – (4.3) задается на максимум, а целевая функция двойственной (4.4) – (4.6) – на минимум.
2. Матрица:
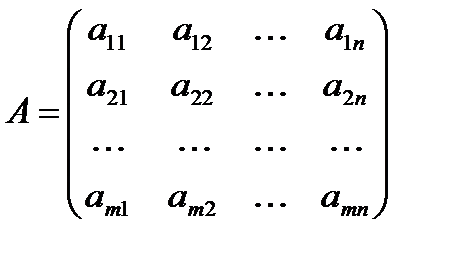, (4.7)
составленная из коэффициентов при неизвестных в системе ограничений (4.2) исходной задачи (4.1) – (4.3), и аналогичная матрица:
(4.8)
в двойственной задаче (4.4) – (4.6) получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов – строками).
3. Число переменных в двойственной задаче (4.4) – (4.6) равно числу ограничений в системе (4.2) исходной задачи (4.1) – (4.3), а число ограничений в системе (4.5) двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (4.4) двойственной задачи (4.4) – (4.6) являются свободные члены в системе (4.2) исходной задачи (4.1) – (4.3), а правыми частями в соотношениях системы (4.5) двойственной задачи – коэффициенты при неизвестных в целевой функции (4.1) исходной задачи.
5. Если переменная xj исходной задачи (4.1) – (4.3) может принимать только лишь положительные значения, то j–е условие в системе (4.5) двойственной задачи (4.4) – (4.6) является неравенством вида “ 
”. Если же переменная xj может принимать как положительные, так и отрицательные значения, то j – соотношение в системе двойственной задачи представляет собой уравнение. Аналогичные связи имеют место между ограничениями (4.2) исходной задачи (4.1) – (4.3) и переменными двойственной задачи (4.4) – (4.6). Если i – соотношение в системе (4.2) исходной задачи является неравенством, то i–я переменная двойственной задачи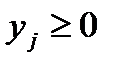 
. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (4.2) прямой задачи и соотношения (4.5) двойственной задачи являются неравенствами вида “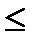 
”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Для практических целей рассмотренные правила позволяют составить следующую схему соответствия.
Таблица 4.1. – Таблица соответствия
| Исходная задача | Двойственная задача |
| Целевая функция максимизируется | Целевая функция минимизируется |
| Константы в правых частях ограничений | Коэффициенты целевой функции |
| Коэффициенты целевой функции | Константы в правых частях ограничений |
| j-й столбец коэффициентов в ограничениях | j-я строка коэффициентов в ограничениях |
| j-я строка коэффициентов в ограничениях | j-й столбец коэффициентов в ограничениях |
| j-я неотрицательная переменная | j-е неравенство вида ≥ |
| j-я переменная, не имеющая ограничений в знаке | j-е соотношение в виде = |
| i-е неравенство вида ≤ | i-я неотрицательная переменная |
| i-е соотношение в виде = | i-я переменная, не имеющая ограничений в знаке |
Дата добавления: 2016-04-02; просмотров: 710;