Математическая модель КТЗ
Пусть 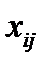 – количество продукции, планируемое к перевозке из пункта Аi в Bj. Тогда, при наличии баланса производства и потребления (5.1) математическая модель транспортной задачи будет выглядеть следующим образом:
– количество продукции, планируемое к перевозке из пункта Аi в Bj. Тогда, при наличии баланса производства и потребления (5.1) математическая модель транспортной задачи будет выглядеть следующим образом:
найти план перевозок
 , где
, где  ;
;  ,
,
минимизирующий общую стоимость всех перевозок
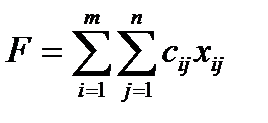 (5.2)
(5.2)
при условии, что из любого пункта производства вывозиться весь продукт
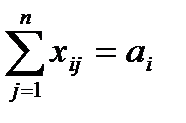 , где
, где  (5.3)
(5.3)
и любому потребителю доставляется необходимое количества груза
 , где
, где  (5.4)
(5.4)
причем, по смыслу задачи
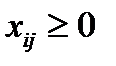 . (5.5)
. (5.5)
Здесь целевая функция (5.2) отражает суммарные транспортные расходы. Ограничения (5.3) требуют, чтобы вся продукция была вывезена, а ограничения (5.4) – чтобы потребности всех пунктов потребления были удовлетворены. Условие (5.5) вытекает из физического смысла введенных переменных.
Ограничения (5.3) – (5.5) задают планы перевозок X. Таким образом, математическая модель КТЗ относится к классу задач линейного программирования.
Для решения транспортной задачи чаще всего применяется метод потенциалов. На каждом шаге происходит переход по определенным правилам от одного базисного решения к другому путем заполнения транспортных таблиц. В данной таблице:
1) строки соответствуют поставщикам (в заголовках строк указываются запасы продукта у поставщиков ai);
2) столбцы соответствуют потребителям (в заголовках столбцов указываются запросы потребителей bj);
3) в клетки заносятся поставки продукта, перевозимого от соответствующего поставщика к соответствующему потребителю (xij);
4) в правом верхнем углу каждой клетки указывается стоимость перевозки единицы продукта от соответствующего поставщика к соответствующему потребителю (cij).
Таблица 5.1 – Транспортная таблица.
| Потребление Производство | b1 | b2 | … | bn | |||
| а1 | с11 | с12 | … | с1n | |||
| x11 | x12 | x1n | |||||
| а2 | с21 | с22 | … | с2n | |||
| x21 | x22 | x2n | |||||
| . . . | . . . | . . . | . . . | ||||
| аm | сm1 | сm2 | … | сmn | |||
| xm1 | xm2 | xmn |
Так как в системе (5.3) – (5.5) ровно (m+n–1) линейно независимых уравнений, то в любой транспортной таблице должно быть m+n–1 занятых клеток.
Дата добавления: 2016-04-02; просмотров: 916;
