Автомодельные решения
Уравнения в частных производных допускают классы упрощенных решений, которые получили название автомодельных. Для решений этого класса характерна зависимость функции решения от одной переменной x, которая является специальной комбинацией t, x.
Для построения примера автомодельного решения рассмотрим одномерное квазилинейное уравнение теплопроводности, в котором коэффициент теплопроводности степенным образом зависит от температуры, т.е.
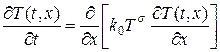, (13)
где k0, s — некоторые неотрицательные константы. Зависимости степенного типа, подобные (13), весьма распространены в физики. Так, в физике плазмы известно, что коэффициент электронной теплопроводности пропорционален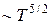 
.
Построим автомодельное решение для уравнения (13) типа бегущей волны:
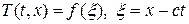. (14)
Подставляя (14) в (13), приходим к следующему обыкновенному дифференциальному уравнению:
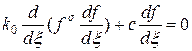. (15)
Уравнение (15) можно один раз проинтегрировать. Появится константа, которую определим, предполагая, что бегущая волна двигается по нулевому температурному фону. После этих предположений возможно провести еще одно интегрирование и в окончательном виде получить:
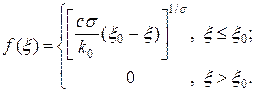(16)
Возвращаясь в (16) к представлению в координатах t, x, получим
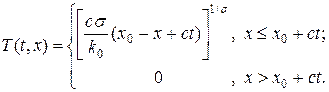(17)
Автомодельное решение (17) представляет собой температурную волну, бегущую с постоянной скоростью по нулевому температурному фону. Фронт волны имеет координату x0 + ct. Профили волны всюду гладкий, кроме фронта волны, где производная терпит разрыв.
На листинге_№2 приведен код программы, изображающей движение бегущей волны (17).
Листинг_№2
%Программа изображения бегущей волны квазилинейного
%уравнения теплопроводности
%очищаем рабочее пространство
clear all
%константы уравнения теплопроводности и бегущей волны
k0=1; sigma=3; c=4; x0=0.5;
%определяем сетки по времени и пространству
t=0:0.025:1;
x=0:0.01:5;
%организуем цикл рисования профиля температуры в
%различные моменты времени
for i=1:length(t)
%определяем профиль температуры
for j=1:length(x)
T(j)=0;
if x(j)<=x0+c*t(i)
T(j)=(((c*sigma)/k0)*(x0-x(j)+...
c*t(i)))^(1/sigma);
end
end
%рисуем температурный профиль
if i==1
plot(x,T,'Color','red','LineWidth',3);
else
plot(x,T);
end
hold on
end
На рис.2 приведены графики, изображающие движение бегущей температурной волны. Красным цветом выделен начальный температурный профиль.
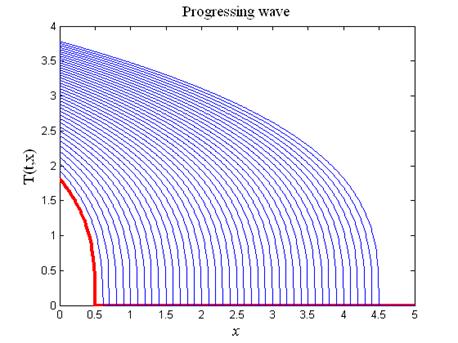
Рис.2. Изображение бегущей волны (17)
Рассмотрим еще один пример автомодельного решения одномерного квазилинейного уравнения теплопроводности с источником:
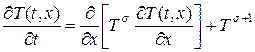. (18)
Уравнение (18) в отличие от (13) содержит источник тепла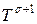 
, степенным образом зависящий от температуры. Согласно исследованиям уравнения (18), проведенных в школе А.А. Самарского и С.П. Курдюмова[3], было установлено наличие так называемой “фундаментальной длины”, на которой происходит горение среды, при этом тепло не распространяется за пределы данной длины, а температура может расти неограниченно в течение конечного интервала времени. Уравнение (18) допускает специальный класс автомодельных решений, который получил название режимов с обострением.
Построим этот класс автомодельных решений. Для этого представим решение в виде:
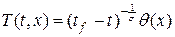. (19)
где tf — время обострения или фокусировки.
Подставим (19) в (18), тогда
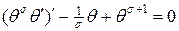. (20)
Уравнение (20) допускает следующее аналитическое решение:
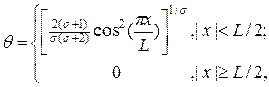(21)
где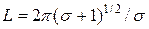 
— фундаментальная длина.
На листинге_№3 приведен код программы, изображающей режим с обострением (19), (21). Итоговый график вынесен на рис.3. Красным цветом на графике выделен начальный профиль.
Листинг_№3
%Программа изображения режима с обострением
%(19), (21)
%очищаем рабочее пространство
clear all
%определяем момент фокусировки и степень
%нелинейности sigma
tf=1; sigma=3;
%определяем фундаментальную длину
L=2*pi*sqrt(sigma+1)/sigma;
%задаем сетки по времени и по пространству
t=0.98:0.001:0.999;
x=-L:0.01:L;
%организуем цикл рисования профиля режима с
%обострением во времени
for i=1:length(t)
for j=1:length(x)
T(j)=0;
if abs(x(j))<0.5*L
T(j)=(tf-t(i))^(-1/sigma)*...
(((2*(sigma+1))/(sigma*(sigma+2)))*...
cos((pi*x(j))/L)^2)^(1/sigma);
end
end
%рисуем температурный профиль в начальный и в
%последующие моменты времени
if i==1
plot(x,T,'Color','red','LineWidth',3);
hold on
end
plo(x,T);
hold on
end
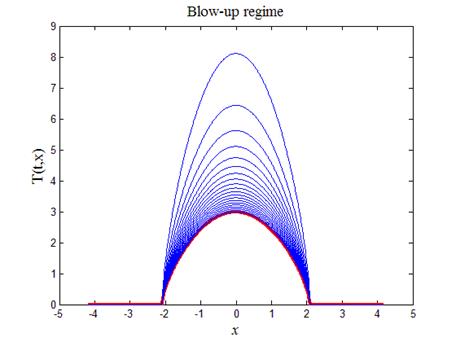
Рис.4. Режим с обострением (19), (21)
Разностный метод
Нелинейные уравнения в частных производных с коэффициентами достаточно общего вида, а также уравнения в областях достаточно общей формы обычно не удается решить аналитическими или автомодельными методами. Основным методом их решения являются численные методы, среди которых наиболее часто используемым является разностный метод.
Для использования разностного метода в области переменных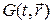 
вводят некоторую сетку. Все производные, входящие в уравнение, заменяют конечными разностями значений функций 
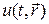в узлах сетки. Полученное в результате алгебраическое уравнение называют разностной схемой. Решая алгебраическую систему уравнений, находят приближенные (разностные) значения функции в узлах сетки. Возникают обычные вопросы при постановке вычислительного эксперимента:
· Существует ли решение алгебраической системы уравнений и является ли оно единственным?
· Каков эффективный алгоритм поиска решения?
· При каких условиях численное решение сходится к точному решению и с какой скоростью?
Есть еще пара вопросов, которые ранее в нашем практикуме не возникали. Это процедура выбора сетки и составление разностной схемы на этой сетке. Для иллюстрации последних двух вопросов рассмотрим пример.
Составим пару простейших разностных схем для линейного одномерного уравнения теплопроводности в ограниченной области G.
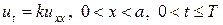, (22)
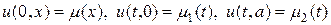. (23)
Решение уравнения теплопроводности (22) с начальными и граничными условиями (23) ищется в ограниченной области G = [0 £ x £ a] ´ [0 £ t £ T].
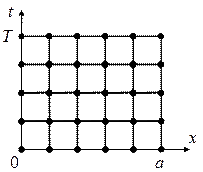
Введем в области G сетку, образованные пересечением прямых линий xn = nh, n = 0,1,…, N и tm = mt, m = 0,1,…,M. Считаем для простоты сетку равномерной по оси x и t соответственно. Величины h и t являются шагами сетки по переменным x и t соответственно (рис.5,а). Значения функции в узлах сетки представим в виде: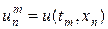 
.
| 
| 
|
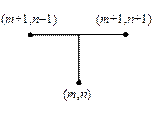
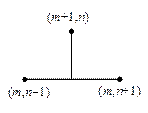
| Рис.5,а. Разностная схема для задачи (22), (23) | Рис.5,б. Шаблон разностной схемы (24), (25) | Рис.5,в. Шаблон разностной схемы (26) |
В начале построим разностную схему для численного решения уравнения (22) следуя конфигурации узлов на рис.5,б. В уравнении (22) заменим производную ut на разностное отношение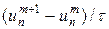 
, а вторую производную uxx — 
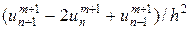. В результате можно получить разностную схему следующего вида
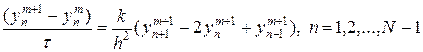(24)
для приближенного решения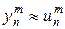 
уравнения (22). Недостающие уравнения для решения задачи (24) берутся из начальных и граничных условий (23), т.е.
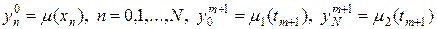. (25)
Конфигурация узлов (рис.5,б) лежащая в основе разностной схемы (24), (25) называется шаблоном.
Для одной и той же задачи можно составить множество разностных схем. Например, если в качестве шаблона разностной схемы выбрать шаблон на рис.5,в, то
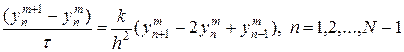. (26)
Начальные и граничные значения для разностной схемы (26) можно записать по аналогии с (25).
В дальнейшем будут рассмотрены различные способы составления и исследования разностных схем для различных типов уравнений. В дальнейших лекциях будут изложены те разностные схемы, которые хорошо себя зарекомендовали при решении тех уравнений математической физики, которые используются в задачах переноса, теплопроводности, диффузии, акустики, газодинамики, электричества и в ряде других областях.
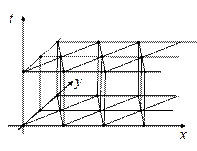
Для большинства разностных схем узлы сетки лежат обычно на пересечении некоторых прямых линий (гиперповерхностей в многомерных задачах). Для двумерных задач в прямоугольной области наиболее часто используют прямоугольную сетку (см., например, рис.5,а). Заметно реже используют треугольную сетку (рис.6,а). Для трехмерных задача наиболее употребительна сетка из прямоугольных параллелепипедов (рис.6,б). На рис.6,в приведен пример менее употребительной трехмерной сетки, состоящей из трехгранных призм.
| 
| 
|
| Рис.6,а. Пример треугольной сетки | Рис.6,б. Пример трехмерной сетки | Рис.6,в. Пример трехмерной сетки |
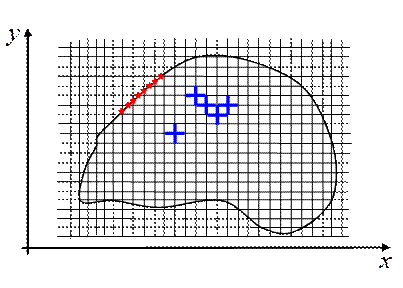
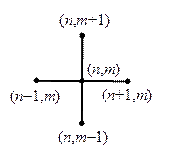
Если одной из переменных в задаче является время t, тогда совокупность узлов сетки, на линии (гиперплоскости) t = tm называют слоем. Узлы разностной схемы связанные друг с другом согласно шаблону называются регулярными, остальные узлы — нерегулярными. Нерегулярными обычно являются граничные узлы. Например, на рис.7,а приведен пример двумерной прямоугольной сетки, на которой построена сложная область с криволинейной границей. Жирным крестом внутри области обозначены регулярные узлы разностной схемы связанные с помощью шаблона, представленного на рис.7,б. Звездами обозначены некоторые нерегулярные узлы в окрестности криволинейной границы области.
| 
|
| Рис.7,а. Пример сложной области и прямоугольной сетки | Рис.7,б. Шаблон разностной сетки |
Вернемся к разностной схеме (26). Положим в этой схеме m = 0, т.к.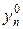 
известно из начального условия, можно найти 
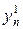при n = 1,…,N-1. Значения 
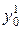и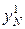 
находим из граничных условий (25). Тем самым значения функции на первом временной слое найдены. Аналогичная процедура может быть проделана при определении 
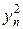и т.д. Схема, похожая на (26), т.е. такая схема, в которой значение функции на следующем слое легко выразить через значения функции на текущем слое называется явной.
Схема (24) на следующем временном слое содержит в каждом уравнении несколько неизвестных значений. Подобные схемы называют неявными. Перепишем схему (24) и граничные условия (25) в следующем виде:
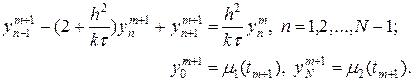(27)
На каждом слое схема (27) представляет собой систему линейных уравнений для определения неизвестных величин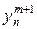 
. Матрица данной алгебраической системы уравнений трехдиагональная и решение может быть найдено с помощью обычной алгебраической прогонки.
Невязка
Рассмотрим операторное уравнение общего вида
Au = f или в иной форме Au - f = 0. (28)
Заменим оператор A разностным оператором Ah, правую часть f — некоторой сеточной функцией jh, а точное решение u — разностным решением y, тогда можно записать разностное схему вида:
Ahy = jh или в другой форме Ahy - jh = 0. (29)
Если в (29) подставить точное решение u, то оно, вообще говоря, не будет удовлетворять уравнению, т.е. Ahu ¹ jh. Величину
y = jh - Ahu = (Au - f) - (Ahu - jh) = (Au - Ahu) - (f - jh).
принято называть невязкой. Для ее оценки обычно используют разложение в ряд Тейлора.
Найдем невязку для явной разностной схемы (26). Перепишем исходное уравнение теплопроводности (22) в форме (28)
.
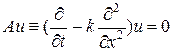Поскольку f = jh = 0, постольку
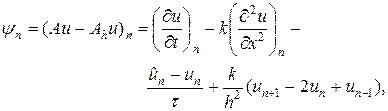(30)
где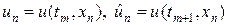 
.
Разложим решение u по формуле Тейлора в окрестности узла (tm,xn), считая что по времени существует вторая непрерывная производная, а по пространству — четвертая непрерывная производная, тогда
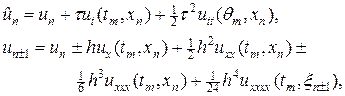(31)
где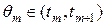 
, 
, 
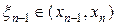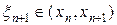. Подставляя (31) в (30) и пренебрегая отличием величин 
, 
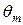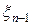и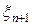 
от tm и xn, находим итоговую оценку невязки
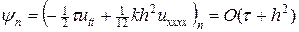. (32)
Согласно (32), невязка стремится к нулю при t ® 0 и h ® 0. Оценка (32) дает оценку невязки в регулярных узлах сетки. Согласно (23), (25), граничные условия выполняются точно, т.е.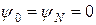 
.
Оценку невязки (32) можно улучшить следующим образом. Найдем utt согласно следующей последовательности выкладок
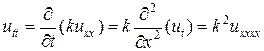. (33)
Подставляя (33) в (32), получим
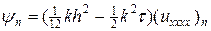. (34)
Согласно формуле (34) можно положить, что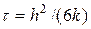 
, тогда главный член невязки (34) обратиться в нуль и останутся члены более высокого порядка малости. Такой прием используется для получения разностных схем повышенного порядка точности.
Дата добавления: 2016-03-27; просмотров: 3729;