Пример решения распределительной задачи
Пример №6.1.
На фабрике эксплуатируются три типа ткацких станков, который могут выпускать четыре вида тканей. Известны следующие данные о производственном процессе:
1) производительности станков по каждому виду ткани, [м/ч]
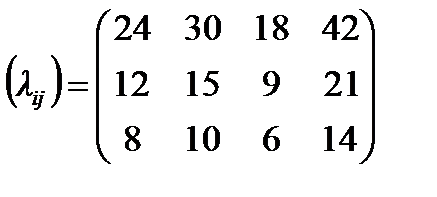 ;
;
2) себестоимость тканей, [руб./м]
 ;
;
3) фонды рабочего времени станков (ai): 90, 220, 180 [ч];
4) планируемый объем выпуска тканей (bj): 1200, 900, 1800, 840 [м].
Требуется распределить выпуск ткани по станкам с целью минимизации общей себестоимости производства ткани.
Решение.
Пусть переменные xij – это время, в течение которого i-й станок будет выпускать j-ю ткань. Распределительная таблица имеет вид:
Распределительная матрица данного примера
| Станки | Ткани | Фонд времени ai, ч | |||||||||||
| B1 | B2 | B3 | B4 | ||||||||||
| A1 | 2 (cij) | 1 | 3 | 1 | 90 | ||||||||
| (lij) 24 | 30 | 18 | 42 | ||||||||||
| A2 | 3 | 2 | 4 | 1 | 220 | ||||||||
| 12 | 15 | 9 | 21 | ||||||||||
| A3 | 6 | 3 | 5 | 2 | 180 | ||||||||
| 8 | 10 | 6 | 14 | ||||||||||
| Объем выпуска bj, м | 1200 | 900 | 1800 | 840 | |||||||||
Целевая функция имеет смысл себестоимости выпуска запланированного количества ткани всех видов
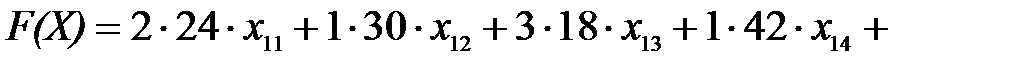
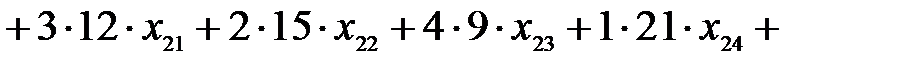
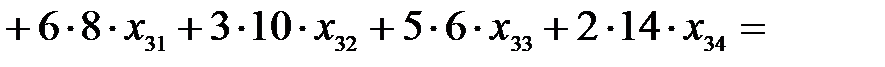

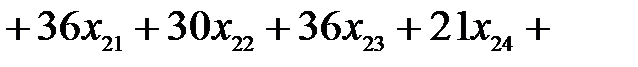
 .
.
Ограничения имеют вид:

Преобразование распределительной задачи в транспортную основано на том, что исходную задачу необходимо представить в виде, когда ткани производит только один станок – базовый и все параметры задачи согласуются с его характеристиками. В качестве базового можно выбирать любой из станков. Пусть это будет станок с максимальной производительностью, т.е. A1. По формуле (6.2) определияются производительности станков 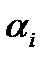 , нормированные относительно производительности базового станка:
, нормированные относительно производительности базового станка:
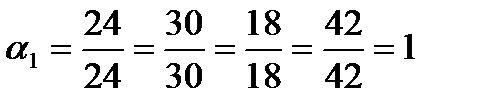 ;
;
 ;
;
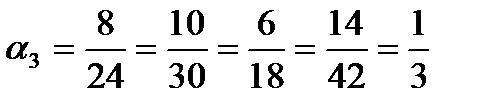 .
.
Таким образом, базовый станок работает в два раза быстрей второго станков и в три раза быстрей третьего.
Пересчет фонда времени станков производится по формуле (6.3):
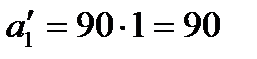 (ч);
(ч); 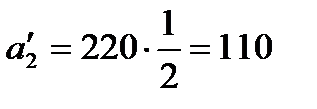 (ч);
(ч);  (ч).
(ч).
Из этих величин следует, что тот объем работ, который второй станок выполняет за свой фонд времени 220 ч, базовый станок сможет выполнить за 110 ч. Аналогично объем работ, который третий станок выполняет за 180 ч, базовый выполнит за 60 ч.
Пересчет планового задания производится по формуле (6.4):
 (ч);
(ч);  (ч);
(ч); 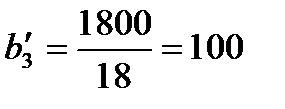 (ч);
(ч);  (ч).
(ч).
Отсюда следует, что план выпуска первого вида ткани базовый станок выполнит за 50 ч, второго вида за 30 ч и т.д.
Пересчет себестоимости производится по формуле (6.5):
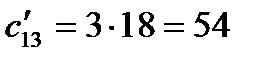 (руб./ч);
(руб./ч); 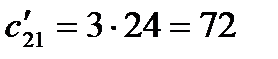 (руб./ч);
(руб./ч); 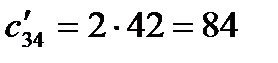 (руб./ч).
(руб./ч).
В полученной транспортной задаче условие баланса (5.1) не выполняется, т.к. суммарный фонд времени станков больше, чем это необходимо для выполнения плана по выпуску всех тканей (260ч > 200ч). Необходимо ввести фиктивный столбец Вф и записать все перечисленные параметры распределительной задачи в транспортную матрицу. Фиктивные тарифы равны нулю.
Транспортная матрица данного примера
| Станки | Ткани | Фонд времени ai, ч | ||||
| B1 | B2 | B3 | B4 | Bф | ||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| Объем выпуска bj, м |
Для упрощения вместо оптимального решения можно рассмотреть опорный план 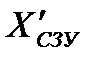 , найденный методом северо-западного угла.
, найденный методом северо-западного угла.
 (ч).
(ч).
После преобразования опорного плана транспортной задачи  в опорный план распределительной задачи
в опорный план распределительной задачи 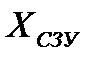 получаем:
получаем:
 (ч).
(ч).
Ответ.
1. Первый станок должен 50 ч производить ткань первого вида, 30 ч – ткань второго вида и 10 ч – ткань третьего вида,
2. Второй станок должен 180 ч производить ткань третьего вида и 40 ч – ткань четвертого вида,
3. Третий станок будет простаивать, не выпуская ткань вообще, т.к. согласно решению, его загрузка находится в фиктивном столбце (x35=180ф).
Определить сколько метров ткани каждого вида должны произвести станки можно по формуле (6.7):
 (м).
(м).
Общая себестоимость производства определяется по формуле (6.1), используя вычисленные значения элементов матрицы 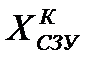
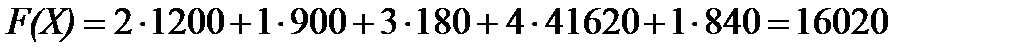 (руб.)
(руб.)
Дата добавления: 2016-04-02; просмотров: 2765;
