В следующих задачах связь между аффинными и однородными координатами считается как в задачах 2, 3.

Найти однородные координаты точки пересечения прямых

2x – 3y + 5 =0, 5x + 2y – 1 = 0.

Решение.

Решим систему уравнений

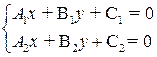
и найдем аффинные координаты 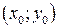точки пересечения прямых.

Мы предполагаем, что система имеет решение. В противном случае прямые не пересекаются на аффинной плоскости.

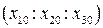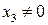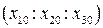
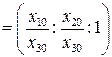
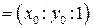Найдем однородные координаты точки пересечения. Так как для конечных точек плоскости , то . Мы воспользовались формулами связи между аффинными и проективными координатами точек.

Итак, однородные координаты точки пересечения прямых имеют вид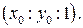

Замечание. Если система не имеет решения, то прямые параллельны на аффинной плоскости. В этом случае их уравнения пропорциональны и можно считать, что прямые задаются уравнениями 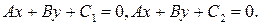На пополненной плоскости они пересекаются в общей несобственной точке .

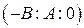Найти аффинные координаты точки пересечения прямых

x1 – 3x2 + 4x3 =0, 5x1 + 2x2 – x3 = 0.

Решение.

Решим систему уравнений

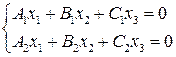
и найдем однородные координаты 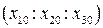их точки пересечения. Они определены с точностью до пропорциональности.

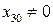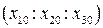
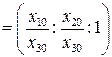
Если , то 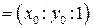. Тогда 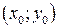- аффинные координаты точки пересечения прямых.

Если 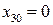, то точка пересечения прямых является несобственной точкой плоскости и не имеет аффинных координат.