Записать аффинное уравнение кривой 2 порядка в однородных координатах и, наоборот, записать однородное уравнение кривой 2 порядка в аффинных координатах.
Решениедля гиперболы.
Рассмотрим каноническое уравнение гиперболы на аффинной плоскости 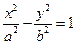 , где
, где 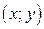 - координаты точек плоскости относительно аффинной системы координат Oe1e2.
- координаты точек плоскости относительно аффинной системы координат Oe1e2.
Пополним плоскость несобственными точками и на пополненной плоскости рассмотрим проективную однородную систему координат R={E1,E2,E3,E}, где O = E3 , а точки E1, E2 порождаются векторамиe1 , e2 .
Формулы связи между аффинными и проективными однородными координатами 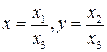 . Подставим
. Подставим 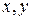 в уравнение гиперболы:
в уравнение гиперболы:
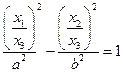 .
.
Умножив уравнение на 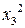 , получим
, получим
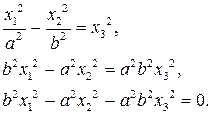
Это уравнение гиперболы на пополненной плоскости в однородных координатах.
Аналогично можно получить уравнения других девяти кривых в однородных координатах на пополненной плоскости
Найти точки пересечения кривых из задачи 1 с несобственной прямой.
Решение
Найдем пересечение гиперболы с бесконечно удаленной прямой. Иными словами, найдем множество бесконечно удаленных точек гиперболы.
Бесконечно удаленная прямая имеет уравнение 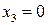 . Следовательно, координаты бесконечно удаленных точек гиперболы удовлетворяют уравнению
. Следовательно, координаты бесконечно удаленных точек гиперболы удовлетворяют уравнению 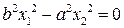 . Решим это уравнение:
. Решим это уравнение:
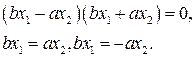
Из последних равенств получаем 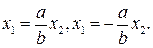
Так как мы получили два решения, то гипербола имеет две бесконечно удаленных точки с координатами
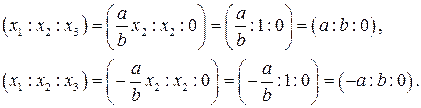
Мы использовали тот факт, что числа  не могут одновременно равняться нулю. Следовательно,
не могут одновременно равняться нулю. Следовательно, 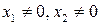 и можно делить координаты на
и можно делить координаты на  В противном случае бесконечно удаленные точки гиперболы имеют координаты
В противном случае бесконечно удаленные точки гиперболы имеют координаты 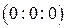 , что невозможно.
, что невозможно.
Напомним, что асимптоты гиперболы имеют уравнения 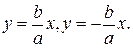 Или в общем виде
Или в общем виде 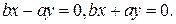 Бесконечно удаленные точки асимптот имеют координаты
Бесконечно удаленные точки асимптот имеют координаты 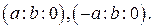
Итак, на пополненной плоскости гипербола пересекается с асимптотами в общих бесконечно удаленных точках.
Даны канонические уравнения эллипса и гиперболы на аффинной плоскости. Записать эти уравнения в однородных координатах и найти проективное преобразование, переводящее кривые друг в друга.
Решение.
1) Рассмотрим канонические уравнения эллипса и гиперболы
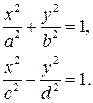
Запишем их в однородных координатах
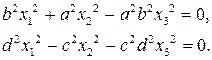
Чтобы найти проективное преобразование, переводящее кривые друг в друга, перепишем уравнения в более удобном виде
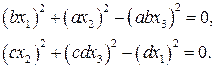
3) Рассмотрим проективное преобразование
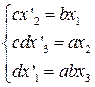 ,
,
т.е. 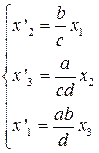 .
.
Оно переводит первую кривую в кривую с уравнением
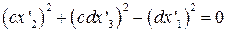 .
.
Штрихи над координатами означают, что полученная кривая является образом первой кривой. После того как образ получен, штрихи можно не писать. Получим уравнение гиперболы в однородных координатах.
Итак, мы нашли проективное преобразование, переводящее эллипс в гиперболу на пополненной плоскости. Напомним, что это невозможно сделать аффинным преобразованием аффинной плоскости. Это означает, что данные кривые принадлежат одному классу проективно эквивалентных кривых.
4. Решить предыдущую задачу для следующих кривых:
Дата добавления: 2016-03-27; просмотров: 1636;
