Элементарные автоматы памяти на основе комбинационного автомата и задержки

Последовательностный автомат может быть синтезирован как композиция комбинационного автомата, реализующего функции переходов φ и выходов ψ и элементарных автоматов памяти , например, задержек на один такт (рис. 64).

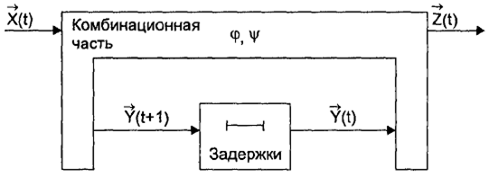
Рис. 64. Задержка на один такт

Физически элементарный автомат памяти типа «задержка на один такт» реализуется линией задержки, которая может быть выполнена в виде специальных элементов — линий задержки или в виде соединения логических элементов, не инверсирующего сигнал, либо, в частных случаях, линией связи, поскольку передача сигнала по ней имеет некоторую конечную длительность, не превышающую длительность такта.

Рассмотрим синтез элементарных автоматов памяти на основе задержек на один такт. Пусть требуется синтезировать автомат, выход которого устанавливается в состояние логической единицы при поступлении сигнала логической единицы на вход установки (обычно он обозначается S — «Set») и хранящий это состояние до поступления сигнала логической единицы на вход сброса (обычно он обозначается R — «Reset»). Таким образом, требуется создать автомат, имеющий два входа R и S и один выход, который обозначим z (рис. 65). Иногда добавляют и инверсный выход .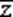

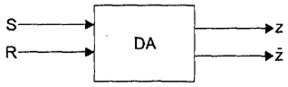
Рис. 65. Элементарный автомат памяти

Ясно, что синтезируется последовательностный автомат, так как его выходной сигнал зависит от последовательности поступления сигналов на входы:

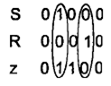
Видно, что при одинаковых входных сигналах на входах SR выходной сигнал может быть как 0, так и 1.

В таком случае опишем функционирование автомата первичной таблицей переходов-выходов (табл. 56).

Таблица 56

Первичная таблица переходов-выходов

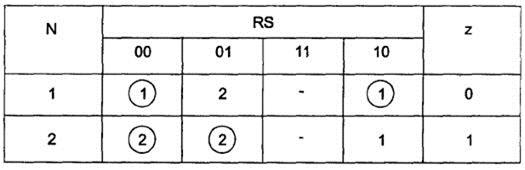
Итак, в исходном состоянии автомат находится в строке с номером 1, в клетке, соответствующей нулевому состоянию RS. При поступлении набора сигналов 01 (начинается установка) автомат начинает переходить в состояние 2 (возникает неустойчивый такт 2), затем происходит перемещение во вторую строку — в устойчивый такт 2, обведенный кружком, при этом на выходе возникает сигнал 1. При поступлении сигнала 10 в первой строке и сигналов 00, 01 во второй строке состояние автомата не меняется, состояние 11 считается невозможным.

Очевидно, что сокращение числа строк табл. 56 невозможно, иначе мы имели бы комбинационный автомат (у которого одно состояние — одна строка).

Приступим к кодированию состояний. Оно в данном случае тривиально: исходное состояние сопоставим с состоянием 0 (1 строка), другое состояние сопоставим с 1.

Получим таблицы переходов-выходов для автомата Мили (табл. 57) и автомата Мура (табл. 58).

Таблица 57

Таблица переходов-выходов элементарного автомата памяти Мили

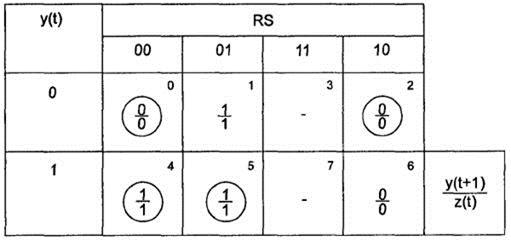
Таблица 58

Таблица переходов-выходов элементарного автомата памяти Мура

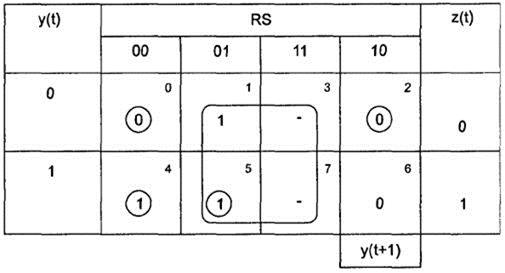
Таким образом, для автомата Мура (см. табл. 58) z(t) = y(t). Построим автомат Мура. Получим функции переходов y(t + 1) и выходов z(t):

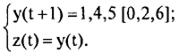
Минимизируя y(t + 1) по карте Карно, какой и является табл. 58, получаем:

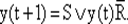
Реализуем эту функцию в виде переключательной схемы (рис. 66).

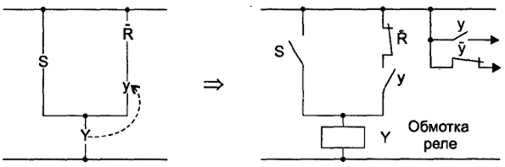
Рис. 66. Переключательные схемы элементарного автомата памяти Мура

На рис. 66 Y — хранитель состояния автомата (например, обмотка реле), обратная связь, указанная пунктиром, реализует самоблокировку. Задержка на один такт осуществляется следующим образом: сначала срабатывает Y, затем замыкается его контакт у. Технически предполагается, что к моменту размыкания S у уже замкнут.

Построим схему на функциональных элементах в базисе И-НЕ:

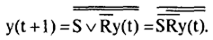
Таким образом, один элемент 2И-НЕ реализует функцию

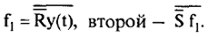
Соответствующая схема показана на рис. 67.

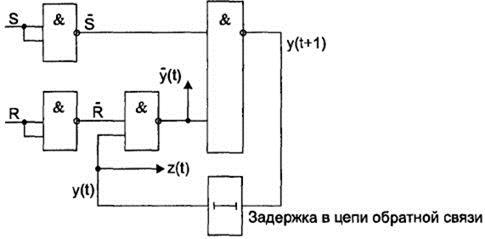
Рис. 67. Реализация элементарного автомата памяти
на функциональных элементах 2И-НЕ

Можно заметить, что выход второго элемента в цепи R при R = 0 соответствует значению 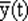. Эту схему часто изображают в несколько другом виде, полагая, что задержка реализуется в линии связи (рис. 68).

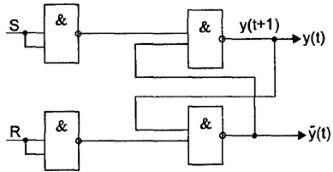
Рис. 68. Условное графическое обозначение RS- триггера

Для описания работы элементарных автоматов памяти применяются таблицы возбуждения, указывающие условия перехода от текущего к последующему внутреннему состоянию.