Регулярные языки и регулярные выражения

В замкнутом полукольце 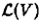всех языков в алфавите V рассмотрим подалгебру , порожденную множеством , которое состоит из пустого языка, языка { λ }, всех языков { a }, а ∈ V (каждый из которых содержит единственную однобуквенную цепочку а ), и замкнутую относительно итерации. Эта подалгебра, обозначаемая 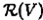, есть полукольцо с итерацией. Оно играет важнейшую роль в теории формальных языков. Его называют полукольцом регулярных языков. Далее будет доказано, что элементы полукольца 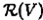являются в точности регулярными языками , т. е. языками, порождаемыми регулярными грамматиками.

Теорема. Язык в алфавите V регулярен тогда и только тогда, когда он является элементом полукольца .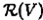

Таким образом, множество регулярных языков в алфавите V = { a 1,..., а n} есть не что иное, как замыкание конечного множества { ∅ , { λ }, { a 1},..., {а n}} относительно операций объединения, соединения и итерации. Следовательно, как и всякое U -замыкание , оно может быть описано индуктивно, а именно:

1) пустое множество ∅ , множество { λ } (состоящее из одной пустой цепочки) и множество { a } для каждого a ∈ V считаем регулярным языком в алфавите V ;

2) если известно, что Р и Q — регулярные языки в алфавите F , то к множеству регулярных языков в алфавите V следует добавить объединение P ∪ Q и соединение PQ ;

3) если известно, что Р — регулярный язык в алфавите V , то к множеству регулярных языков в алфавите V следует добавить его итерацию Р* ;

4) никаких других регулярных языков, кроме определенных в пп. 1–3, не существует.

Позитивная итерация регулярного языка регулярна.

Алгебраические операции над регулярными языками удобно представлять с помощью так называемых регулярных выражений. Каждое регулярное выражение представляет (или обозначает) некоторый (однозначно определяемый) регулярный язык, причем языки ∅ , { λ } и {а }, где а ∈ V , обозначаются выражениями ∅ , λ и а соответственно, и если регулярное выражение р обозначает регулярный язык Р , а регулярное выражение q обозначает регулярный язык Q , то регулярные выражения ( p + q ), ( pq ) и (р* ) обозначают регулярные множества Р ∪ Q , PQ и Р* соответственно. Таким образом, в регулярных выражениях для обозначения операции объединения языков используют знак «+» (плюс).

Все регулярные выражения , фигурирующие в этих преобразованиях, эквивалентны , т. е. все они обозначают один и тот же регулярный язык. Проблемы распознавания эквивалентности двух произвольных регулярных выражении, автоматизации тождественных преобразований регулярных выражений и поиск самого короткого («оптимального») регулярного выражения, обозначающего данный регулярный язык, весьма трудны и здесь не обсуждаются. В целом соотношение между регулярными выражениями и регулярными языками вполне аналогично соотношению между формулами и булевыми функциями . В частности, если переход от формулы к эквивалентной формуле в теории булевых функций совершается согласно аксиомам булевой алгебры и другим тождествам, выводимым из этих аксиом, то переход от заданного регулярного выражения к эквивалентному регулярному выражению производится согласно аксиомам полукольца и тождествам, выводимым из них.

Зачастую в дальнейшем, если это не повлечет непонимания, мы будем отождествлять регулярный язык с обозначающим его регулярным выражением (любым!), что позволит не вводить новых обозначений и пояснений. Так, для рассмотренного выше примера мы можем написать bbababbb ∈ ( b +а )* b * , что, строго говоря, обозначает факт принадлежности цепочки bbababbb языку, обозначенному регулярным выражением ( b +a )* b *. Разумеется, следует воздерживаться, например, от употребления такой записи: λ ∈ λ , хотя, если подумать, и здесь все понятно: пустая цепочка λ принадлежит языку { λ }, обозначаемому регулярным выражением λ .

Цит. по: Дискретная математика: учебник для вузов /
А.И. Белоусов, С.Б. Ткачев; под ред. В.С. Зарубина, А.П. Крищенко. —
3-е изд., стереотип. — М.: Изд-во МГТУ им. Баумана, 2004. — С. 462–470, 486–494. —
(Сер. Математика в техническом университете; Вып. XIX).