Классификация грамматик и языков

Напомним, что единственное ограничение, накладываемое на правило вывода любой грамматики, состоит в том, что в левую часть правила должен входить хотя бы один нетерминал. В зависимости от дополнительных ограничений, накладываемых на правила вывода грамматики , различают следующие основные классы грамматик.

1. Грамматики типа 0 , или грамматики общего вида.Здесь на правила вывода не накладывается никаких дополнительных ограничений.

2. Неукорачивающие грамматики . Каждое правило такой грамматики имеет вид α → β , где |α| ≤ | β |. Таким образом, длина правой части правила не меньше длины левой.

3. Контекстно-зависимые грамматики (КЗ-грамматики ).Грамматику называют контекстно-зависимой грамматикой (КЗ-грамматикой), если любое ее правило вывода имеет вид φ A ψ → φ ξ ψ, где А — нетерминал , ξ — некоторая цепочка, ξ ≠ λ . Каждое такое правило, называемое КЗ-правилом, позволяет заменить нетерминал А в «контексте», образуемом цепочками φ и ψ в объединенном алфавите , непустой цепочкой ξ . Иногда цепочку φ называют левым контекстом, а цепочку ψ — правым контекстомданного КЗ-правила. Из определения видно, что каждая КЗ-грамматика является неукорачивающей.

Если в КЗ-правиле снять требование непустоты цепочки ξ , то получим грамматику, которую называют обобщенной КЗ-грамматикой(или, коротко, ОКЗ-грамматикой).

4. Контекстно-свободные грамматики (КС-грамматики ). Каждое правило такой грамматики имеет вид А → α, т. е. левая часть каждого правила вывода есть нетерминал, а правая — произвольная (может быть и пустая) цепочка в объединенном алфавите.

С практической точки зрения это наиболее важный класс грамматик, поскольку именно в терминах КС-грамматик описывается синтаксис языков программирования.

5. Линейные грамматики . Каждое правило такой грамматики имеет вид А → uBv или А → u , т. е. в правой части правила может содержаться не более одного вхождения нетерминала. Если во всех правилах вида А → uBv имеет место v = λ , то грамматика называется праволинейной , а если и = λ — леволинейной.

Пример 7.6.Линейной является грамматика

где множество правил вывода Р 6есть

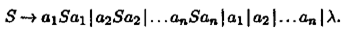
6. Регулярные грамматики. У такой грамматики каждое правило имеет вид А → αВ или А → α, где α есть либо терминал, либо пустая цепочка. Регулярные грамматики — частный случай праволинейных грамматик.

Приведем без доказательства некоторые утверждения о классах грамматик.

Теорема. Для любой грамматики типа 0 может быть построена эквивалентная ей ОКЗ-грамматика.

2. Для любой неукорачивающей грамматики может быть построена эквивалентная ей КЗ-грамматика.

3. Для любой леволинейной грамматики может быть построена эквивалентная ей праволинейная грамматика, и, наоборот, для любой праволинейной грамматики может быть построена эквивалентная ей леволинейная грамматика.

4. Для любой праволинейной грамматики может быть построена эквивалентная ей регулярная грамматика.

Классификация языков, порождаемых грамматиками, тесно связана с классификацией самих грамматик, хотя и не тождественна ей. Язык относят к классу С , если существует грамматика класса С, порождающая данный язык. Таким образом определяются языки типа 0, неукорачивающие языки , контекстно-зависимые языки (КЗ-языки ), обобщенные контекстно-зависимые языки (ОКЗ-языки ), контекстно-свободные языки (КС-языки ), линейные языки , право- и леволинейные языки , регулярные языки.

Итак, можно утверждать, что имеют место следующие строгие включения классов языков:

РЕГ ⊂ ЛИН ⊂ КС ⊂ ОКЗ = ТИП 0; КЗ ⊂ ОКЗ,

где РЕГ, ЛИН, КС, КЗ, ОКЗ, ТИП 0 — классы регулярных, линейных, КС-языков, КЗ-языков, ОКЗ-языков и языков типа 0 соответственно.

Принципиальное различие между классификацией грамматик и языков состоит в следующем. Чтобы определить класс грамматики, достаточно посмотреть на множество ее правил вывода. Чтобы доказать «положительное» утверждение о том, что заданный язык есть язык такого-то класса, достаточно придумать любую грамматику из соответствующего класса, которая его порождает. Но чтобы доказать «отрицательное» утверждение о классе языка, т. е. доказать, что язык не принадлежит такому-то классу языков, нужно доказать, что не существует грамматики соответствующего класса, которая его порождает. Эта задача гораздо труднее.