I.4. Классификация САР

Системы автоматического регулирования можно классифицировать по различным признакам.

А. По отсутствию или наличию вспомогательной энергии, поступающей в систему от внешних специальных источников, различают САР

-прямого действия,

-непрямого действия.

У САР прямого действия мощности сигнала, выдаваемого датчиком регулируемой величины z, хватает для приведения в действие регулирующего устройства. У САР непрямого действия этой мощности не хватает, поэтому в этом случае сигнал с датчика выходной величины необходимо усилить, для чего необходим посторонний источник вспомогательной энергии.

Б. По количеству входных и выходных (регулируемых) координат системы подразделяются на

-одномерные САР;

-многомерные САР.

САР с одним входным и одним выходным сигналом принято называть одномерными. САР с несколькими входами и выходами называют многомерными.

В. По виду дифференциальных уравнений, описывающих процессы в системах, различают

-линейные САР;

-нелинейные САР.

Линейной системой называется такая система, динамика всех элементов которой вполне описывается линейными уравнениями (алгебраическими или дифференциальными). Для этого необходимо, прежде всего, чтобы статические характеристики всех элементов системы были линейные, т.е. имели вид прямой линии как на рис. I.9 а, б.

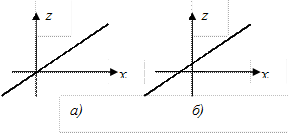
Рис. I 9. Статические характеристики

линейных элементов.

Нелинейной системой называется такая система, в которой хотя бы в одном элементе нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики элемента (произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных и их производных).

Если линейная (нелинейная) система характеризуется постоянными параметрами, то ее поведение описывается линейными (нелинейными) дифференциальными уравнениями с постоянными коэффициентами. Если в уравнении динамики какого-либо элемента линейной (нелинейной) системы имеется хотя бы один или несколько переменных, с зависящими от времени коэффициентами, то получается линейная (нелинейная) система с переменными параметрами. Если какой-либо элемент описывается линейным (нелинейным) уравнением в частных производных (например, имеют место волновые процессы в трубопроводе или в электрической линии), то, значит, речь идет о линейной (нелинейной) системе с распределёнными параметрами (во всех предыдущих случаях имели место системы со средоточенными параметрами). Если динамика какого-либо элемента системы описывается линейным (нелинейным) уравнением с запаздывающим аргументом (т.е. элемент обладает чисто временным запаздыванием или временной задержкой передачи сигнала), то система называется линейной (нелинейной) системой с запаздыванием.

Г. По способу передачи сигналов различают следующие САР

-непрерывные;

- дискретные (импульсные, цифровые);

-релейные

Непрерывная САР характеризуется наличием только непрерывных (аналоговых) сигналов. Под непрерывным (аналоговым) сигналом понимается случай, когда непрерывному изменению аргумента (обычно это время) соответствует непрерывное изменение сигнала (рис. I.10)

Наряду с непрерывным способом передачи и преобразования сигнала в настоящее время широко применяются дискретные способы, в которых используются в том или ином виде дискретизация сигнала. Дискретизация сигнала состоит в замене непрерывного сигнала теми или иными дискретными его значениями и может быть осуществлена по времени, по уровню либо по времени и по уровню одновременно.

Дискретизация сигнала по времени, или квантование по времени, соответствует выделению значений сигнала в заранее фисксированные моменты времени, называемые моментами квантования. Обычно эти

моменты времени отстоят друг от друга на постоянную величину

T = const, называемую интервалом или периодом квантования по времени (рис. I.11). В этом случае непрерывный сигнал (пунктир на рис. I.11) заменяется совокупностью ординат (дискрет), определяемых в моменты квантования. Понятно, что при этом часть информации об аналоговом сигнале, относящаяся ко времени между точками квантования, утрачивается. Если в системе хотя бы один сигнал квантован по времени и нет других видов квантования, то такая система называется импульсной.

Дискретизация сигнала по уровню, или квантование по уровню, соответствует выделению значений сигнала при достижении им заранее фиксированных уровней. Эти фиксированные уровни сигнала обычно

Рис. I.11. Квантование сигнала по времени

отстоят друг от друга на постоянную величину σ = const, называемую интервалом квантования по уровню (рис.I.12)

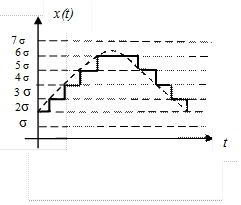
Рис 1.12. Квантование сигнала по уровню

В этом случае аналоговый сигнал с определённым приближением, зависящим от величины s, заменяется некоторой ступенчатой функцией.

Если в системе хотя бы один сигнал квантован по уровню и нет других видов квантования, то такая система называется релейной.

И, наконец, дискретизация сигнала и по времени и по уровню одновременно соответствует выделению в заранее фиксированные моменты времени значений сигнала, ближайших к заранее фиксированным уровням (рис. I.13).

В предлагаемом случае аналоговый сигнал приближенно может быть представлен совокупностью цифр, каждая из которых отображает в

момент квантования номер уровня, ближайшего к значению аналогового сигнала. В данном случае речь идет о следующей совокупности цифр: 2, 3, 4, 4, 5, 4, 2 . . . Если в системе хотя бы один сигнал квантован и по времени и по уровню одновременно и нет других видов квантования, то такая система называется цифровой.

Д. По рассогласованию в установившемся режиме различают системы

- статические,

- астатические.

САР называется статической, если в ней установившеесязначение выходной величины не остается постоянным, а меняется при изменении нагрузки. В такой системе обязательно присутствует не равная нулю статическая ошибка D_ст ¹ 0.

САР называется астатической, если в ней установившееся значение выходной величины не зависит от нагрузки. В такой системе статическая ошибка равна нулю D_ст = 0.

Е. По способу задания регулируемой (выходной) величины различают системы

- стабилизации,

- программные,

- следящие.

Под системами стабилизации понимают САР, предназначенные для стабилизации (т.е. поддержания постоянным) выходного (регулируемого) сигнала. Широко распространены САР стабилизации температуры, угловой скорости, напряжения и т.п.

В системах программного управления программа изменения во времени входного сигнала задана заранее, а выходной сигнал должен отслеживать (повторять) изменение входного. В качестве примера такой системы можно назвать станок с числовым программным управлением. Программа работы выходного устройства станка – режущего инструмента – заранее для каждого вида детали записана на материальном носителе (перфокарте, магнитной ленте, диске и т.п.) и является входным сигналом станка. Режущий инструмент станка, выполняя эту программу, изготовляет соответствующую деталь. Таким образом, выходной сигнал (перемещение режущего инструмента) повторяет заданную программу, т.е. копирует заранее известный входной сигнал.

В следящих системах выходной сигнал также копирует входной сигнал, который, однако, может изменяться по произвольному, заранее неизвестному закону. Примером следящей системы может служить система управления зенитным орудием. Зенитное орудие достаточно громоздко и тяжело и перемещают его обычно с помощью электрического привода. Это орудие располагается в зоне противовоздушной обороны объекта и предназначено для поражения воздушной цели противника, которая, как правило, в зоне ПВО совершает противозенитные маневры. Для наблюдения за целью оператор зенитной установки использует легкое и подвижное визирное устройство, связанное следящей системой с зенитным орудием. Наводя визирное устройство на подвижную цель, оператор тем самым через следящую систему наводит на эту цель зенитное орудие и в нужный момент производит выстрел. Итак, здесь зенитное орудие повторяет движение визирного устройства, которое зависит от движения цели и заранее неизвестно.

Существуют и другие направления классификации систем автоматического регулирования, но для наших целей мы ограничимся вышерассмотренными.