Существование невычислимых по Тьюрингу функций.

Теорема 36.1. Существует функция , не вычислимая по Тьюрингу , т. е. не вычислимая ни на одной машине Тьюринга.

Доказательство . Функции, о которых идет речь, представляют собой функции, заданные и принимающие значения в множестве слов в алфавите А 1= {1}. Ясно, что множество слов в алфавите А 1= {1} счетно. Следовательно, рассматривается множество всех функций, заданных на счетном множестве и принимающих значения в счетном же множестве. Как известно, это множество имеет мощность континуума. С другой стороны, поскольку множество всевозможных машин Тьюринга, как мы установили в предыдущем пункте, перенумеровав их, счетно, это и множество функций, вычислимых по Тьюрингу, также счетно. Континуальная мощность строго больше счетной. Следовательно, существуют функции, не вычислимые по Тьюрингу.

Доказанная теорема есть чистая теорема существования. Интересно получить пример конкретной функции, не вычислимой по Тьюрингу.

Пример 36.2. Укажем конкретную функцию, которую нельзя вычислить ни на какой машине Тьюринга. На основании тезиса Тьюринга это будет означать, что не существует вообще никакого алгоритма для вычисления значений такой функции.

Рассмотрим следующую функцию ψ (α ) на словах в алфавите А 1= {1}. Для произвольного слова α длиной п в алфавите А 1= {1} положим: ψ(α) = βnI , если слово α перерабатывается машиной Тьюринга с номером п () в слово βnалфавита А 1= {1}; ψ(α) = 1 в противном случае. Докажем, что функция ψ (α ) не вычислима по Тьюрингу.

Допустим противное. Это означает, что существует машина Тьюринга T стандартным алфавитом {a 0, 1, q , П, Л}, вычисляющая эту функцию. Пусть k — номер этой машины в нумерации, описанной в предыдущем пункте. Посмотрим, чему равно слово ψ(1k) (напомним, что 1k= 11...1 — слово из k единиц), являющееся значением функции ψ (α ) при α = 1k. Предположим, что машина Т перерабатывает слово 1kв слово βkв том же алфавите А 1= {1}. Тогда по определению вычислимости функции ψ (α ) на машине T это означает, что ψ(1k) = βk. Но с другой стороны, по самому определению функции ψ (α ) это означает, что ψ(1k) = βk1. Полученное противоречие доказывает, что машины Тьюринга, вычисляющей функцию ψ (α ), не существует.

Принимая во внимание тезис Тьюринга, заключаем, что не существует вообще никакого алгоритма для вычисления значений функции ψ (α ). Это означает, что массовая проблема нахождения значений функции ψ (α ) для всевозможных значений аргумента алгоритмически не разрешима.

Проблемы распознавания самоприменимости и применимости.Это еще два примера алгоритмически не разрешимых проблем. Сначала о первой. Предположим, что на ленте машины Тьюринга записана ее собственная функциональная схема в алфавите машины. Если машина применима к такой конфигурации, то будем называть ее самоприменяемой, в противном случае — несамоприменяемой. Возникает массовая проблема распознавания самоприменяемых машин Тьюринга, состоящая в следующем. По заданной Функциональной схеме (программе) машины Тьюринга установить, к какому классу относится машина: к классу самоприменимых машин или к классу несамоприменимых машин.

Теорема 36.3.Проблема распознавания самоприменимых машин Тьюринга алгоритмически не разрешима.

Доказательство . Допустим противное, т. е. алгоритм для такого распознавания существует. Значит, на основании тезиса Тьюринга, существует машина Тьюринга, реализующая данный алгоритм. Пусть Θ — такая машина. На ее ленту заносится соответствующим образом закодированная программа той или иной машины Тьюринга. При этом, если машина самоприменима, то занесенное слово перерабатывается машиной Θ в какой-то символ σ (имеющий смысл утвердительного ответа на поставленный вопрос о самоприменимости). Если же машина несамоприменима, то занесенное на ленту слово, кодирующее ее программу, перерабатывается машиной Θ в какой-то символ τ (имеющий смысл отрицательного ответа на поставленный вопрос).

Рассмотрим теперь такую машину Тьюринга Θ1, которая по-прежнему перерабатывает несамоприменимые коды в τ, а к самоприменимым кодам машина Θ1уже не применима. Такая машина получается из машины Θ, если следующим образом слегка изменить ее программу: после появления символа σ вместо остановки машина должна неограниченно его повторять.

Итак, Θ1применима ко всякому несамоприменимому коду (вырабатывая символ τ) и не применима к самоприменимым кодам. Это приводит к противоречию, потому что такая машина не может быть ни самоприменимой, ни несамоприменимой. В самом деле, если машина Θ1самоприменима, то она не применима к своему коду. Значит, машина несамоприменима. Противоречие. С другой стороны, если машина Θ1несамоприменима, то ее код должен перерабатываться самой машиной Θ1в символ τ. Значит, Θ1применима к собственному коду, т. е. самоприменима. Снова противоречие. Оно и доказывает теорему.

На основании доказанной теоремы устанавливается алгоритмическая неразрешимость и некоторых других массовых проблем, возникающих в теории машин Тьюринга, например проблема распознавания применимости для машин Тьюринга , которая состоит в следующем. Заданы функциональная схема (программа) какой-нибудь машины Тьюринга и конфигурация в ней: узнать, применима ли машина к данной конфигурации или нет.

Теорема 36.4. Проблема распознавания применимых машин Тьюринга алгоритмически не разрешима.

Доказательство . Если бы существовал алгоритм для решения этой проблемы, то с его помощью можно было бы узнать, применима ли машина к слову, кодирующему ее собственную программу, т. е. самоприменима ли она. Но на основании предыдущей теоремы известно, что такого алгоритма не существует.

Алгоритмически неразрешимые проблемы в общей теории алгоритмов.Итак, мы установили алгоритмическую неразрешимость двух проблем, связанных с машинами Тьюринга: проблема распознавания самоприменимых машин Тьюринга (теорема 36.3) и проблема распознавания применимости для машин Тьюринга (теорема 36.4). Каждое из этих утверждений может быть сформулировано и доказано и в общей теории алгоритмов (в инвариантном виде).

Теорема о неразрешимости проблемы остановки (т. е. проблемы распознавания применимости алгоритма) звучит так. Не существует алгоритма, который по номеру х любого алгоритма (в произвольной, но фиксированной нумерации) и исходным данным у определял бы, остановится алгоритм при этих данных или нет; иначе говоря, не существует алгоритма В (х , у ) , такого, что для любого алгоритма Ах(с номером φ–1(A ) = x ).

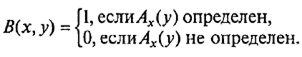
Теорему об алгоритмической неразрешимости проблемы самоприменимости алгоритмов можно сформулировать так. Не существует алгоритма В 1(х ) такого, что для любого алгоритма Ах

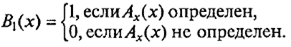
Рассмотрим еще одну алгоритмическую проблему об алгоритмах и докажем ее неразрешимость. Это проблема определения общерекурсивности алгоритмов (и функций ), т. е. проблема определения того, ко всяким ли допустимым начальным данным применим алгоритм. .

Теорема 36.6. Проблема определения общерекурсивности алгоритмов неразрешима , т. е. не существует алгоритма В (х ), такого , что для любого алгоритма Ах

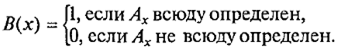
Доказательство . Допустим противное, т. е. такой алгоритм В (х ) существует. Тогда он определяет общерекурсивную функцию f (x ). Определим функцию g (x ) следующим образом:

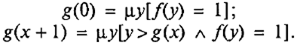
Так как номеров всюду определенных функций (и, следовательно, точек у , в которых f (y ) = 1) бесконечное множество, то функция g (x ) всюду определена. Ясно, что функция g (x ) принимает значение 1 на каждой всюду определенной вычислимой (т. е. общерекурсивной) функции, т. е. является перечислением множества всех общерекурсивных функций. Но, на основании предыдущей леммы, такого перечисления не существует. Противоречие. Следовательно, не существует и алгоритма В (х ), определенного в условии теоремы, т. е. проблема определения общерекурсивности алгоритмов неразрешима.

Раз нельзя указать единого алгоритма, отличающего всюду определенные вычислимые (т. е. общерекурсивные) функции от частично рекурсивных, попытаемся подойти к проблеме частично рекурсивных функций с другой стороны. Может быть, возможно каждую частично рекурсивную функцию доопределить на неопределимых точках так, чтобы получилась рекурсивная (т. е. общерекурсивная) функция. Оказывается, и эта задача неразрешима, что следует из теоремы, приведенной ниже.

Теорема 36. 7. Существует такая частично рекурсивная функция f , что никакая общерекурсивная функция g не является ее доопределением .

Доказательство . Как и прежде, считаем, что выбрана некоторая вычислимая нумерация φ: N → А l * и для каждого алгоритма Ахзначение φ–1(Ax) = x — его номер в этой нумерации. Рассмотрим следующую частичную функцию:

Ясно, что функция f (x ) вычислима и, значит, частично рекурсивна.

Пусть теперь g (x ) — произвольная общерекурсивная функция и xg— ее номер в нумерации φ, т. е. φ–1(g ) = xg. Так как g всюду определена, то 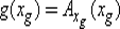определена и, следовательно, f (xg) = g (xg) + 1. Таким образом, для любой общерекурсивной функции g имеем f (xg) ≠ g (xg). Это и означает, что f ≠ g . Теорема доказана.

Следовательно, существуют частичные алгоритмы, которые нельзя доопределить до всюду определенных алгоритмов.

Теорема Райса.Эта теорема описывает в рамках общей теории алгоритмов еще один достаточно обширный круг алгоритмически не разрешимых проблем. Рассмотренные ранее подобные проблемы носили довольно экзотический характер: все они были так или иначе связаны с самоприменимостью алгоритма, когда алгоритм работает с собственным описанием (находится значение вычислимой функции fxв точке, являющейся ее собственным номером в выбранной нумерации вычислимых функций: fx(x )). Теорема Райса, опираясь на неразрешимость этой проблемы, устанавливает алгоритмическую неразрешимость вообще всякого нетривиального свойства вычислимых функций.

По-прежнему имеется некоторая нумерация алгоритмов φ: N → А l * , в которой каждый алгоритм Ахимеет номер φ–1(Ax) = x . Этот же номер имеет и функция fx, которую вычисляет алгоритм Ах. (Следует помнить, что одна и та же функция, будучи вычисляема разными алгоритмами, может иметь в данной нумерации много номеров. Но это обстоятельство не влияет на нижеследующую теорему.)

Теорема 36.8 (Райc ). Пусть С — любой непустой собственный класс вычислимых функций от одного аргумента (существуют как функции , принадлежащие С , так и вычислимые функции , не принадлежащие С ). Тогда не существует алгоритма , который бы по номеру х функции fxопределял бы , принадлежит f хклассу С или нет. Иначе говоря , множество {х : fxÎ С} неразрешимо.

Доказательство . Допустим противное, т. е. множество {х : fxÎ С} разрешимо. Тогда оно обладает вычислимой характеристической функцией:

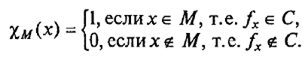
Пусть f 0— нигде не определенная функция. Рассмотрим сначала случай, когда f 0Ï С. Выберем тогда какую-нибудь конкретную вычислимую функцию faÎ С и определим функцию F (x , у ):

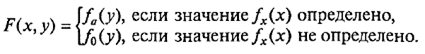
Функция F (x , у ) вычислима. Для ее вычисления надо вычислять fx(x ): если fx(x ) определена, то этот процесс когда-нибудь остановится и нужно будет перейти к вычислению fa(y ); если же fx(x ) не определена, то процесс не остановится, что равносильно вычислению функции f 0(y ).

Зафиксируем в функции F (x , у ) аргумент х . Тогда F станет вычислимой функцией от одного аргумента у. Номер этой функции в единой нумерации φ вычислимых функций зависит от значения x , т. е. является всюду определенной функцией g (x ). Ясно, что функция g (x ) вычислима, так как является суперпозицией двух вычислимых функций: g (x ) = φ –l(F (x , у )). Таким образом, F (x , у ) = fg(x)(y ) и, значит,

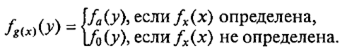
Отсюда ясно, fg(x)Î С тогда и только тогда, когда fg(x)= fa(так как faÎ С), т. е. fx(x ) определена. (В случае же, когда fx(x ) не определена, мы имеем fg(x)= f 0 и, следовательно, fg(x)Ï С , так как f 0Ï С.) Другими словами, g (x ) Î М тогда и только тогда, когда fx(x ) определена. Это означает, что характеристическая функция χMна аргументах g (x ) имеет вид:

Последнее означает следующее. Поскольку функции χMи g вычислимы, то мы для каждого номера х можем выяснить, определено значение fx(x ) или нет. Это, в свою очередь, означает, что построена разрешающая функция χM◦ g для проблемы самоприменимости алгоритма, что невозможно.

Если рассмотреть случай, когда f 0Î С, то нужно выбрать faÏ С. Проведя аналогичные рассуждения, придем к следующей разрешающей функции для проблемы самоприменимости 1 – χM(g (x )), что также противоречит доказанной ранее неразрешимости этой алгоритмической проблемы. Теорема доказана.

Теорема Райса означает, что не существует единого алгоритма, который для каждой вычислимой функции (по ее номеру) определял бы, обладает эта функция тем или иным свойством или нет, например, является ли эта функция постоянной, монотонной, периодической, ограниченной и т. п. Но это лишь первое приближение к пониманию смысла этой теоремы. Дело в том, что мы пытаемся создать единый алгоритм, который имеет дело с функциями. Но что значит иметь дело с функцией? Функция должна быть как-то задана. В данном случае функция fxзадается вычисляющим ее алгоритмом Ах(мы помним, что каждая функция может вычисляться множеством алгоритмов). Разыскиваемый нами единый алгоритм как раз и имеет дело с алгоритмами, вычисляющими функции. Так вот, смысл теоремы Райса состоит в том, что по описанию алгоритма, вычисляющего функцию, ничего нельзя узнать о свойствах функции, которую он вычисляет. Еще раз подчеркнем — не существует единого алгоритма, применимого к описаниям всех вычисляющих алгоритмов.

В частности, оказывается неразрешимой проблема эквивалентности алгоритмов (): по двум заданным алгоритмам нельзя узнать, вычисляют они одну и ту же функцию или нет.

Каждый, кто имел дело с программированием (написанием компьютерных программ), знает, что по тексту сколько-нибудь сложной программы, не запуская ее в работу, трудно понять, что она делает (какую функцию вычисляет). Если это понимание и приходит, то каждый раз по-своему; единого метода здесь не существует. Это своего рода практическое проявление теоремы Райса.

Мы уже обсуждали проблемы синтаксиса и семантики языка при рассмотрении формальных теорий. В теории алгоритмов появляется еще один аспект этой проблемы. Синтаксические свойства алгоритма — это свойства описывающих его текстов, т. е. свойства конечных слов в фиксированном алфавите. Семантические (или смысловые) свойства алгоритма связаны с тем, что он делает. Хорошо известно, что в процессе отладки программ синтаксические ошибки отыскиваются довольно легко (этому, в частности, способствуют и дополнительные программы-алгоритмы). Главные неприятности связаны именно с анализом семантики неотлаженной программы, т. е. с попытками установить, что же она делает вместо того, чтобы делать то, что мы хотим (и здесь нам уже никакие дополнительные программы помочь не могут). Образно выражаясь, можно сказать, что теорема Райса звучит так: по синтаксису алгоритма ничего нельзя узнать о его семантике.

Цит. по: Математическая логика и теория алгоритмов:
учебное пособие для студентов высших учебных заведений /
В. И. Игошин. — 2-е изд. стер. — М.: Издательский центр «Академия», 2008. — С. 366–376.

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат,1988. — 450 с.

Аляев Ю.А.Алгоритмизация и языки программирования Pascal , C++, Visual Basic : Учеб. справ. пособие / Ю.А. Аляев, О.А. Козлов. — М.: Финансы и статистика, 2004. — 320 с.

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат,1988. — 450 с.

Там же.

Горбатов В.А. Основы дискретной математики / Учеб. пособие для вузов. — М: Высшая школа, 1986. — 312 с.

Энциклопедия. Т. 22. Информатика / Глав. ред. Е А Хабалина, вед. науч. ред. А.Г. Леонов. — М.: Аванта, 2003. — 624 с.