Интегрирование некоторых иррациональных функций.
1. Интегралы вида òR(x, (ax + b) m1/n1, (ax + b) m2/n2, …)dx, гдеR– рациональная функция, а mi, ni,– целые числа, вычисляются с помощью подстановки ах + b = ts, где s – наименьшее общее кратное чисел ni.
Пример:

где 
2. Интегралы вида 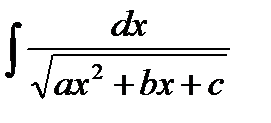 сводятся к табличным выделением полного квадрата в подкоренном выражении.
сводятся к табличным выделением полного квадрата в подкоренном выражении.
Пример: 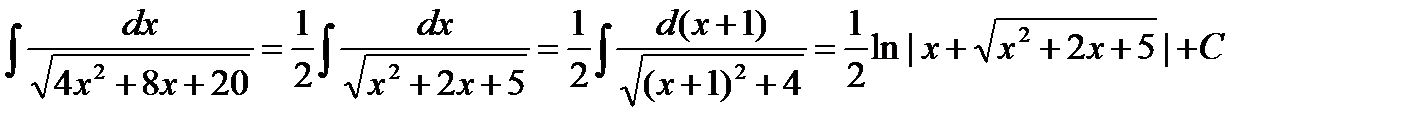
3. Интегралы вида 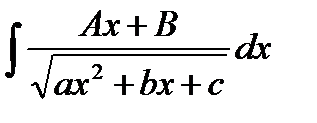 вычисляются с помощью известного уже приема – в числителе выделяют производную подкоренного выражения и интеграл представляют в виде суммы более простых интегралов.
вычисляются с помощью известного уже приема – в числителе выделяют производную подкоренного выражения и интеграл представляют в виде суммы более простых интегралов.
Пример: 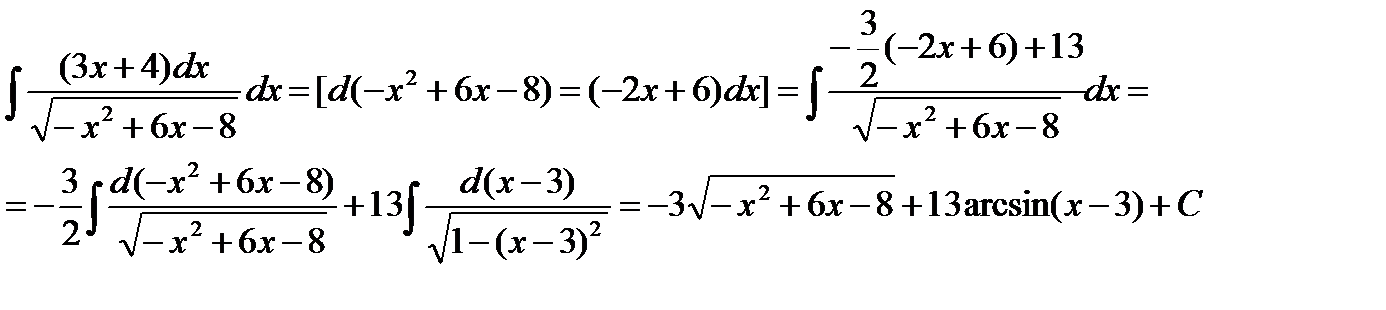
3. Интеграл вида  с помощью подстановки х – a = 1/t сводится к интегралу, рассмотренному ранее.
с помощью подстановки х – a = 1/t сводится к интегралу, рассмотренному ранее.
Пример:
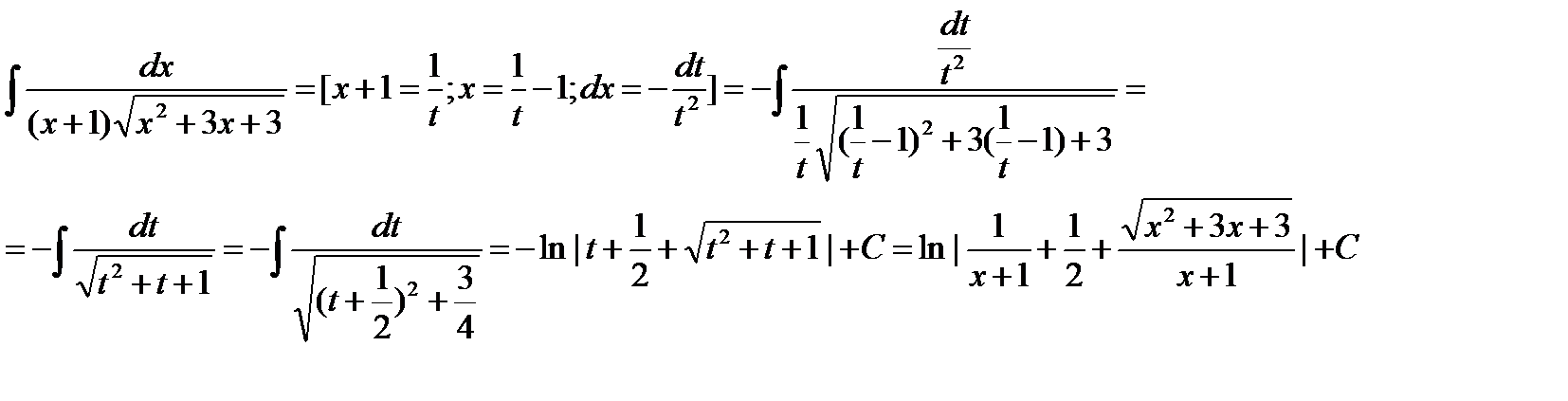
5. Интегралы вида  ,
, 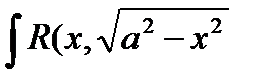 ,
,  приводятся к интегралам от рациональных относительно sint (cost) функций с помощью надлежащей тригонометрической подстановки: для первого
приводятся к интегралам от рациональных относительно sint (cost) функций с помощью надлежащей тригонометрической подстановки: для первого
х =а sect (х = а cosect), для второго х = а sint (х = а cost) и для третьего
х = а tgt (x = a ctgt).
Пример: 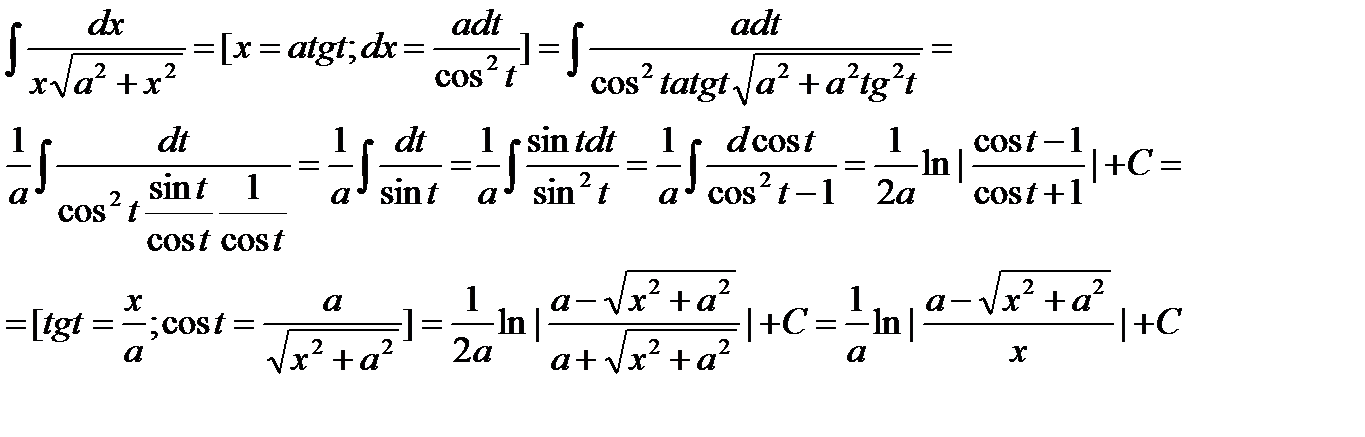
Контрольные вопросы.
1) Как найти интегралы вида 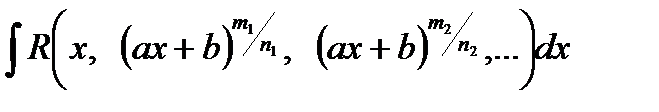 , где R – рациональная функция, а mi, ni – целые числа?
, где R – рациональная функция, а mi, ni – целые числа?
2) Как найти интегралы вида 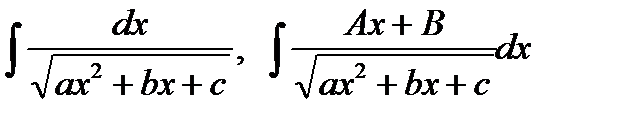 ?
?
3) Как найти интегралы вида 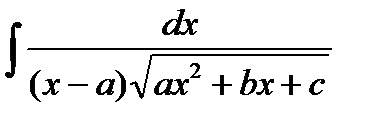 ?
?
4) Как найти интегралы вида 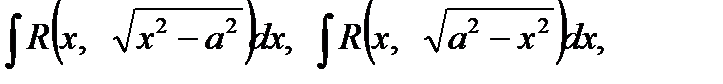
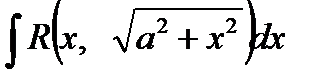 ?
?
Тест 25.
Найти неопределённые интегралы и выбрать верные ответы:
1) 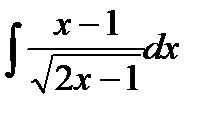 ; 2)
; 2) 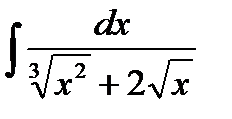 .
.
1) а) 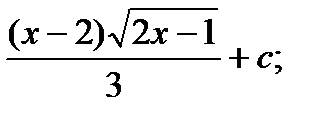 б)
б) 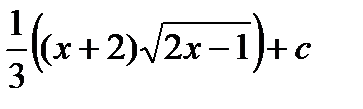 .
.
2) а)  б)
б) 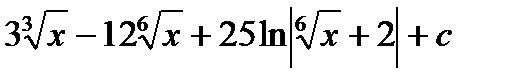 .
.
Дата добавления: 2016-04-14; просмотров: 1413;
