О «неберущихся» интегралах
Выше говорилось, что если и выполняются условия существования первообразной, то не всегда она может быть найдена как конечная комбинация элементарных функций. Соответствующий интеграл можно рассматривать как новую неэлементарную функцию. Такие функции часто носят название специальных, многие из них хорошо изучены (и табулированы). Например, та из первообразных 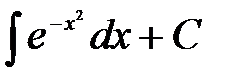 , которая обращается в нуль при х = 0 называется функцией Гаусса и обозначается Ф(х), т.е. Ф(х) =
, которая обращается в нуль при х = 0 называется функцией Гаусса и обозначается Ф(х), т.е. Ф(х) = 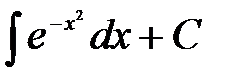 если Ф(0) = 0. (Представление о том, как с помощью элементарных функций можно представить и вычислить «неберущиеся» интегралы можно будет получить в разделе 10. «Ряды»).
если Ф(0) = 0. (Представление о том, как с помощью элементарных функций можно представить и вычислить «неберущиеся» интегралы можно будет получить в разделе 10. «Ряды»).
Контрольные вопросы.
1) Приведите примеры «неберущихся» интегралов.
2) Какая функция называется функцией Гаусса, как она определяется?
Итоговый тест.
1. Решить систему однородных уравнений  и выбрать верный ответ: а)
и выбрать верный ответ: а) 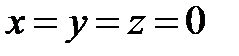 ; б)
; б) 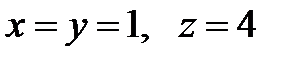 .
.
2. Найти матрицу, обратную данной и указать верный ответ: 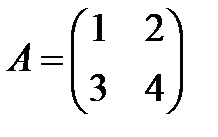 ;
;
а)  ; б)
; б)  .
.
3. Найти ранг матрицы и выбрать верный ответ:  .
.
4. Определить угол между векторами 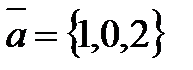 и
и 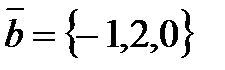 и выбрать верный ответ: а)
и выбрать верный ответ: а) 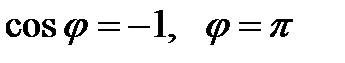 ; б)
; б) 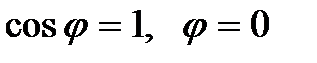 .
.
5. Определить параметры k и b уравнения прямой 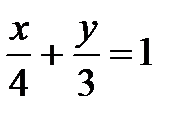 и выбрать верный ответ: а)
и выбрать верный ответ: а) 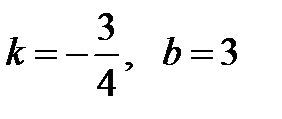 ; б)
; б) 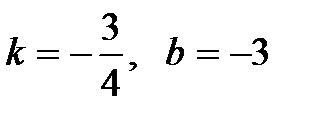 .
.
6. Определить, какие линии задаются уравнениями: 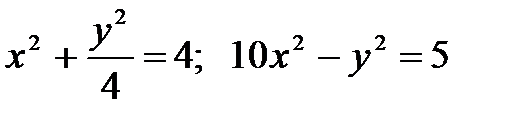 и выбрать верный ответ:
и выбрать верный ответ:
а) окружность и гипербола; б) эллипс и гипербола.
7. Найти нормальный вектор плоскости 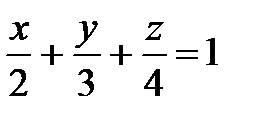 и выбрать верный ответ: а)
и выбрать верный ответ: а)  ; б)
; б) 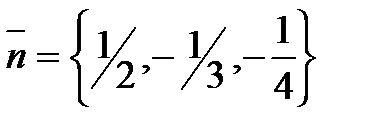 .
.
8. Найти точку пересечения прямой с плоскостью:  и выбрать верный ответ:
и выбрать верный ответ:
а) (6,4,5); б) (6,-4,5).
9. Найти центр и радиус сферы 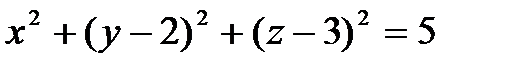 и выбрать верный ответ: а) С(0,2,3), R=
и выбрать верный ответ: а) С(0,2,3), R= 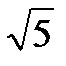 ; б) С(0,-2,-3), R=
; б) С(0,-2,-3), R= 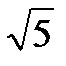 ;
;
10. Найти 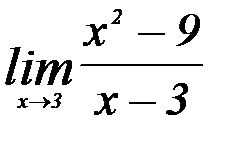 .
.
а) 6; б) 0; в) 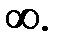
11. Функция в данной точке дифференцируема, то :
а) функция разрывается в этой точке; б) функция непрерывна в этой точке.
12. В каких типах неопределённостей, для раскрытия которых может быть использовано правило Лопиталя:
а) 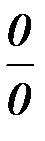 ; б)
; б)  ; в)
; в) 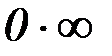 ; г)
; г)  .
.
13. Может ли формула Тейлора применена для раскрытия неопределённостей вида 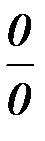 и
и  ?
?
а) может; б) не может; в) только для вида 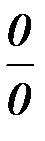 .
.
14. Если для функции y=ax3+bx2+cx+d выполняется условие3ас>b2(при любом d), то:
а) функция имеет максимум; б) функция имеет минимум;
в) функция не имеет экстремума.
15. Дана функция 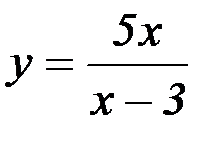 . Является ли х=3 уравнением асимптоты и если является, то какого вида?
. Является ли х=3 уравнением асимптоты и если является, то какого вида?
а) является, горизонтальная асимптота; б) является, вертикальная асимптота;
в) является, наклонная асимптота; г) не является асимптотой.
16. При каком условии функция z=f(x,y) принимает в точке (х,у) max:
а) 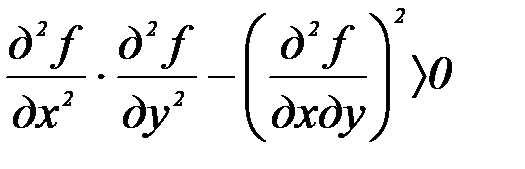 и
и  ; б)
; б) 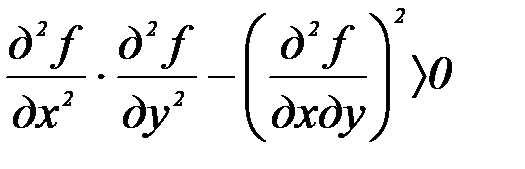 и
и 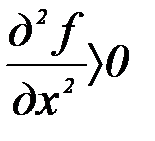 ;
;
в) 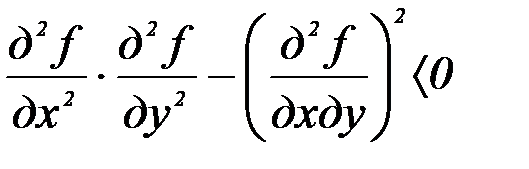 ; г)
; г) 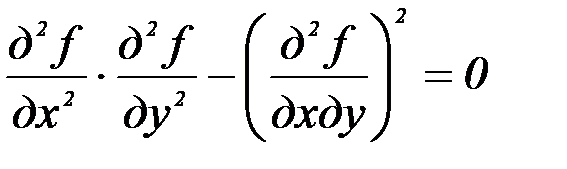 .
.
17. Указать целесообразную подстановку для отыскания интегралов
1) 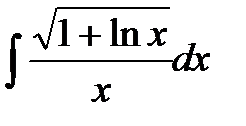 , 2)
, 2)  и выбрать верный ответ:
и выбрать верный ответ:
1) а)  ; б)
; б) 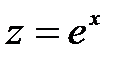 ; 2) а)
; 2) а) 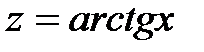 ; б)
; б) 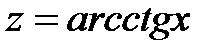 .
.
18. Каким способом следует найти 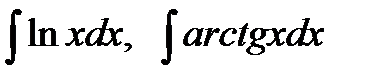 ?
?
а) по частям; б) подстановкой
19. Найти интеграл, выбрать верный ответ: 
а) 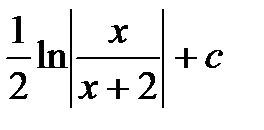 ; б)
; б) 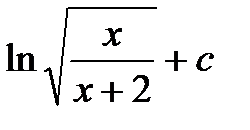 .
.
20. Найти 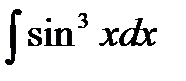 .
.
а)  ; б)
; б) 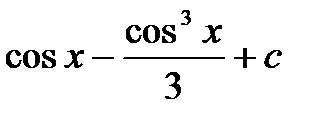 .
.
Вопросы для самопроверки.
1. Решение систем линейных уравнений методом Крамера; матричным методом; методом Гаусса.
2. Векторы. Скалярное, векторное и смешанное произведение векторов.
3. Собственные векторы и собственные значения матрицы.
4. Линейные преобразования. Квадратичные формы.
5. Прямая на плоскости. Различные уравнения. Угол между прямыми.
6. Кривые второго порядка (эллипс, гипербола, парабола).
7. Плоскость в пространстве. Различные способы задания.
8. Прямая в пространстве. Способы задания. Условия параллельности и перпендикулярности прямых; прямой и плоскости. Поверхности второго порядка их изображение.
9. Функция. Область её определения, способы задания. Основные элементарные функции и их графики.
10. Предел. Определение предела функции. Основные свойства предела. Бесконечно малые и бесконечно большие величины. Основные теоремы о пределах. Два замечательных предела. Число е. Натуральные логарифмы.
11. Непрерывность функции. Непрерывность элементарных функций. Свойства функций, непрерывных на отрезке.
12. Производная и дифференциал одной переменной. Приращение аргумента и функции. Определение производной.
13. Правила нахождения производных. Таблица производных основных элементарных функций.
14. понятие о сложной функции. Определение дифференциала. Производная высших порядков.
15. Теорема о среднем. Правило Лопиталя. Формула Тейлора.
16. Исследование функций с помощью производных.
17. Элементы дифференциальной геометрии.
18. Функции нескольких переменных. Основные определения. Частные производные. Дифференциалы.
19. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала.
20. Скалярное поле. Производная по направлению. Градиент.
21. Экстремум функции двух независимых переменных.
22. Метод наименьших квадратов.
23. Условный экстремум функции нескольких переменных.
24. Определение неопределённого интеграла. Непосредственное интегрирование. Метод подстановки.
25. Интегрирование методом по частям
26. Интегрирование рациональных функций. Интегрирование выражений 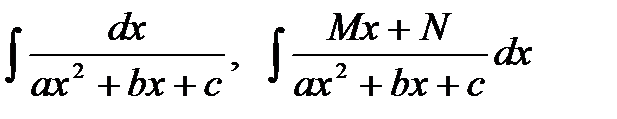 .
.
27. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.
28. Интегрирование некоторых иррациональных функций:  ,
, 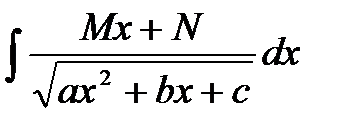 .
.
29. О неберущихся интегралах. Функция Гаусса.
Ответы на тесты
Тест 1 1) б. 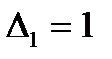 ; 2) б.
; 2) б. 
Тест 2 1) 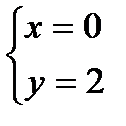 ; 2)
; 2) 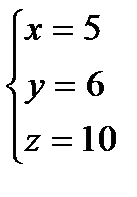
Тест 3 б)
Тест 4 б)
Тест 5 1) а.  2) а.
2) а.
Тест 6 1) а; 2) а.
Тест 7 1) а. 135о ; 2) б. 24,5
Тест 8 1) а. 14 куб. ед.; 2) а. да
Тест 9 1) а. 9 кв. ед.; 2) 1) а; 2) а; 3) б; 4) а.
Тест 10 1) а; 2) б; 3) б; 4) 1) а., 2) а.
Тест 11 1) а; 2) б.
Тест 12 1) б; 2) а и б - оба
Тест 13 1) а; 2) а.
Тест 14 1) а; 2) б.
Тест 15 1) б, т.к. 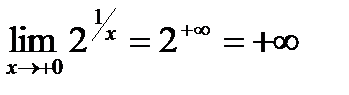 ; 2) в.
; 2) в.
Тест 16 1) а; 2) в; 3) г; 4) г; 5) в; 6) б.
Тест 17 1) а; 2) г, т.к. 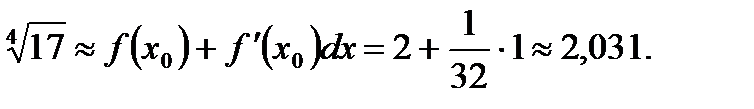
Тест 18 1) а; 2) б; 3) а; 4) в; 5) б.
Тест 19 1) в; 2) а; 3) б.
Тест 20 1) а; 2) б, т.к 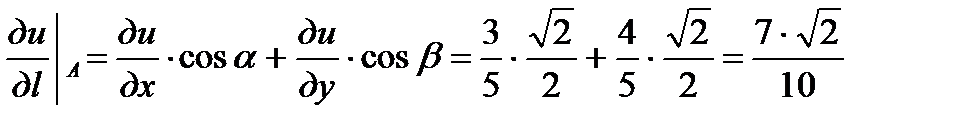
Тест 21 1) а; 2) а.
Тест 22 1) б; 2) а.
Тест 23 1) а; и б; (оба) ; 2) а.
Тест 24 1) а; 2) а.
Тест 25 1) а; 2) а.
Дата добавления: 2016-04-14; просмотров: 1084;
