Интегрирование тригонометрических функций.
1. Интегралы вида òsinmx cosnx dx
а) Если хотя бы один из показателей m и n – нечетное положительное число – используются подстановки sinx = t при нечетном n и cosx = t при нечетном m.
Примеры:
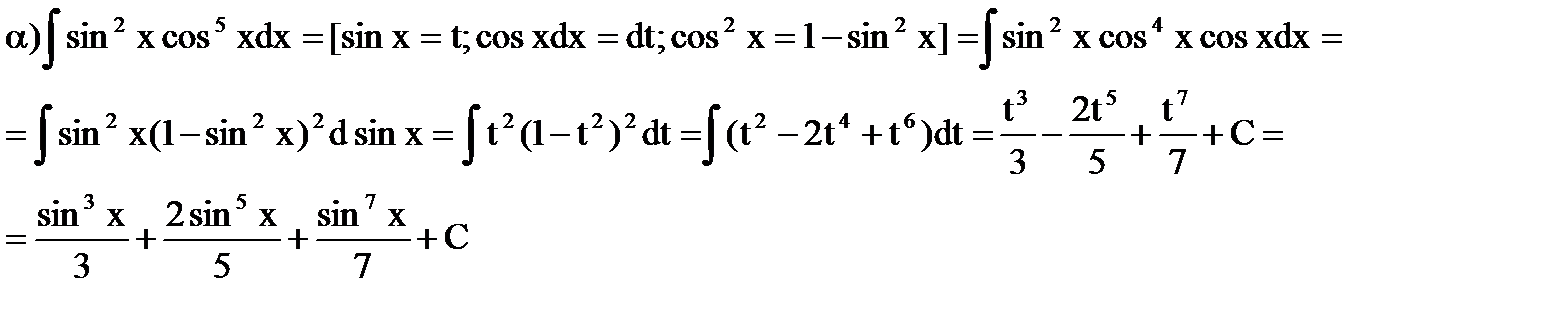
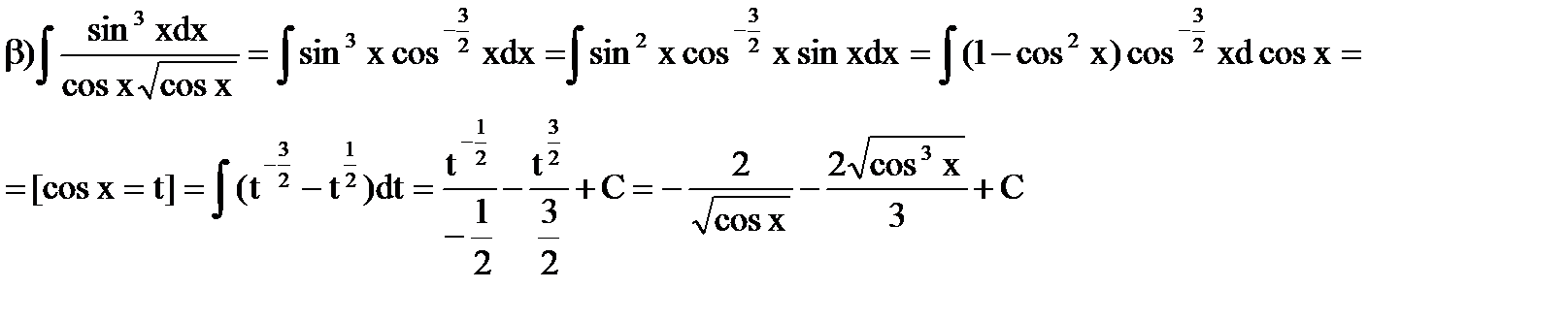
б) Если оба показателя m и n – четные положительные числа, подинтегральную функцию следует преобразовать с помощью известных соотношений: 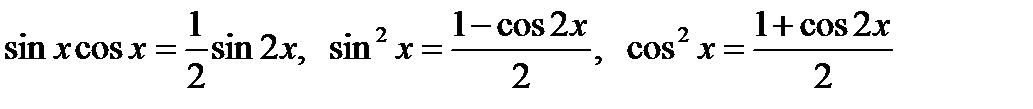 .
.
Пример: 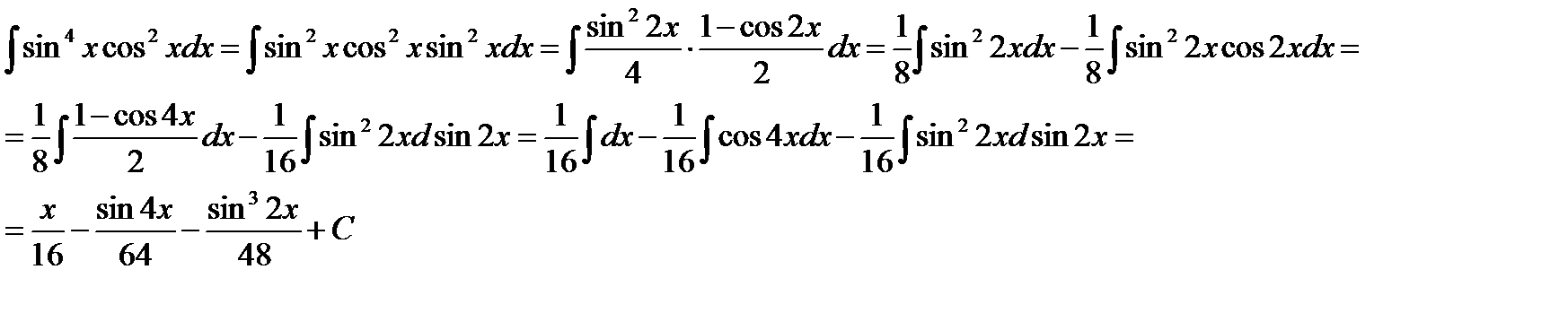
2. Интегралы вида òtgmxdx и òctgmxdx, где m – целое положительное число, интегрируются с помощью соотношений tg2x = sec2x–1 и ctg2x = cosec2x – 1, позволяющих последовательно понижать степень подинтегральной функции.
Пример:
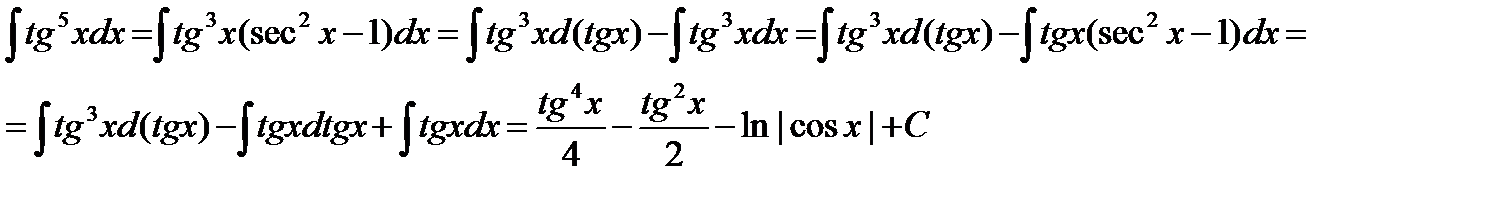
Аналогично находятся интегралы вида òtgmx secnx dx и òctgmx cosecnx dx, где n – целое положительное число.
Интегралы òsin(mx) cos(nx) dx, òcos(mx) cos(nx) dx, òsin(mx) sin(nx) dx вычисляются с помощью формул sina cosb = ½[sin(a +b) + sin(a – b)], cosa cosb = ½[cos(a + b) + cos(a – b)], sina sinb = ½[cos(a – b) – cos (a + b)], позволяющих произведение тригонометрических функций представить в виде суммы.
Интегралы вида òR(sinx, cosx)dx, где R – рациональная функция, вычисляются с помощью универсальной тригонометрической подстановки tg x/2 = t (х = 2arctgt). Переход к новой переменной в подинтегральном выражении осуществляется с помощью формул:
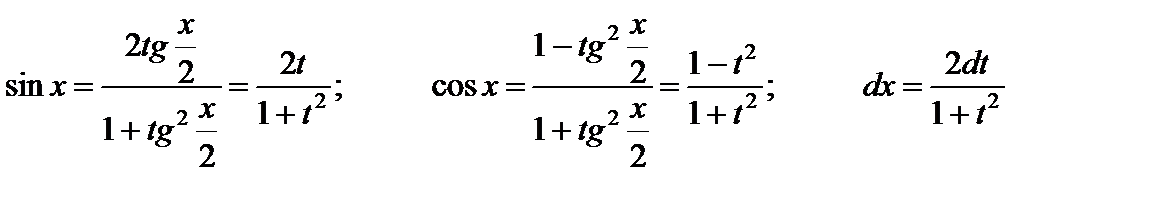 (5.26)
(5.26)
Пример: 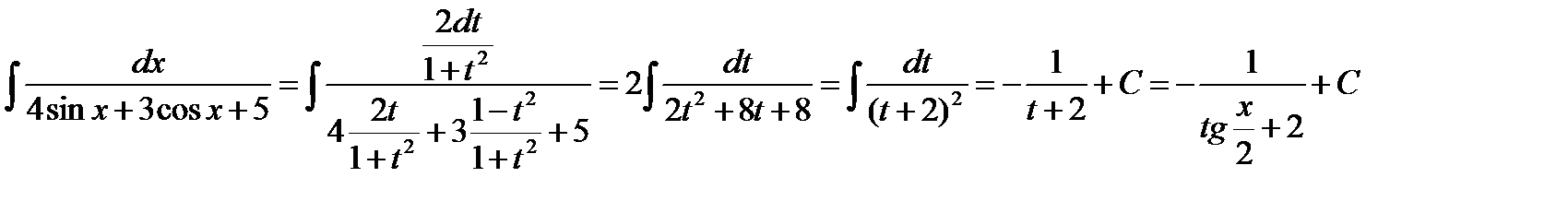
Проинтегрируем с помощью тригонометрической подстановки простейшую рациональную дробь четвёртого типа 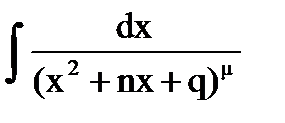 , где
, где  . Выделив в знаменателе полный квадрат получим
. Выделив в знаменателе полный квадрат получим 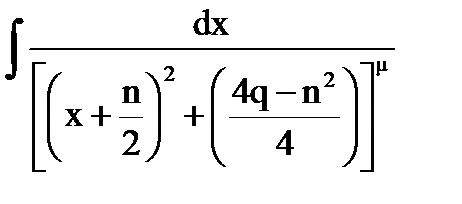 и, обозначив
и, обозначив 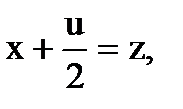

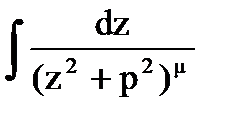 . Применив подстановку
. Применив подстановку 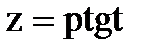
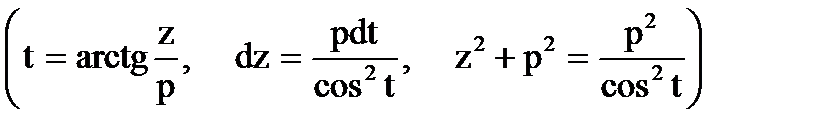 получим
получим  легко вычисляемый уже известным приёмом.
легко вычисляемый уже известным приёмом.
Контрольные вопросы.
1) Как найти интегралы вида 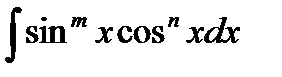 , если: а) хотя бы один из показателей m или n – нечётное положительное число; б) оба показателя m и n – чётные положительные числа?
, если: а) хотя бы один из показателей m или n – нечётное положительное число; б) оба показателя m и n – чётные положительные числа?
2) Как найти интегралы вида 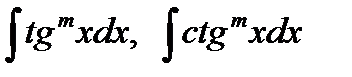 , где m – целое положительное число?
, где m – целое положительное число?
3) Как найти интегралы вида 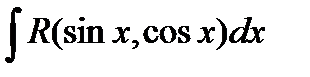 , где R – рациональная функция?
, где R – рациональная функция?
Тест 24.
Найти интегралы и указать верные ответы: 1) 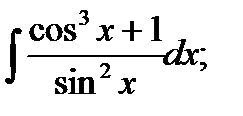 2)
2) 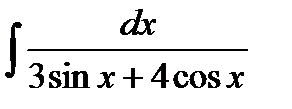 .
.
1) а) 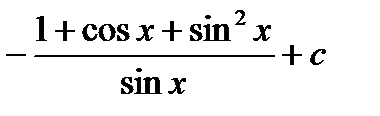 ; б)
; б) 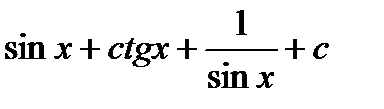 ;
;
2) а) 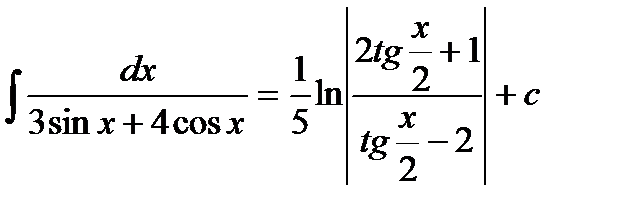 ; б)
; б) 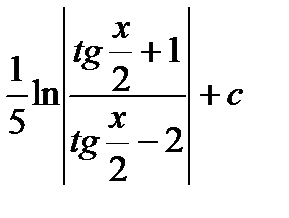 .
.
Дата добавления: 2016-04-14; просмотров: 1284;
