Интегрирование дробно-рациональных функций

Пусть 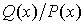есть правильная рациональная дробь, у которой 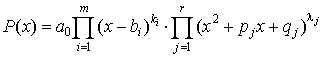. Тогда, согласно предыдущим теоремам, ее можно представить в виде

,

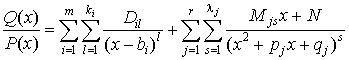которое называется разложением правильной рациональной дроби на простейшие.

Для нахождения коэффициентов разложения стандартным является следующий алгоритм:

1. Написать разложение рациональной дроби на простейшие с неопределенными коэффициентами.

2. Привести правую часть получившегося выражения к общему знаменателю, раскрыть скобки и собрать члены с одинаковыми степенями х.

3. Приравнять коэффициенты при одинаковых степенях х в знаменателях получившейся и исходной дроби.

4. Решить получившуюся систему линейных алгебраических уравнений и найти все неопределенные коэффициенты.

В результате интеграл распадется на сумму интегралов следующих типов:

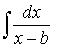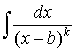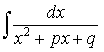, , , и , .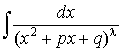

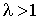Все они вычисляются в явном виде. Имеем

, .

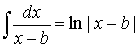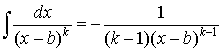Запоминать явные выражения для интегралов двух последних типов не надо.

Определенный интеграл