Связь выпуклости (вогнутости) функции с поведением ее производной

Теорема.Пусть f(x) определена и непрерывна на [a, b] и 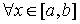имеет конечную производную. Для того, чтобы f(x) была выпуклой (вогнутой) необходимо и достаточно, чтобы 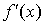монотонно возрастала (убывала).

Следствие.Пусть f(x) и 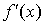непрерывны на [a, b] и 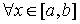существует 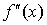. Тогда для того, чтобы f(x) была выпуклой (вогнутой) необходимо и достаточно, чтобы ( ).

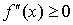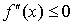Точка перегиба

Определение.Точка x₀ называется точкой перегибафункции f(x) если она отделяет участок, где f(x) выпукла от участка, где f(x) вогнута.

Рис. 3.9 Вид графика функции в окрестности точки перегиба

Вид графика функции в окрестности точки перегиба приведен на рис. 3.9. Обратите внимание на то, что касательная проведенная к кривой в точке перегиба пересекаеткривую.

Необходимое условие точки перегиба. Если x₀ – точка перегиба функции f(x), то в ней выполняется условие .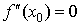

Достаточное условие точки перегиба.Если выполнено условие 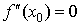, то это еще не означает, что x₀ – точка перегиба функции f(x). Для выяснения того, как выглядит график функции в окрестности этой точки надо найти первую по порядку старшинства производную, отличную от нуля 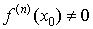, причем должно быть 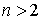. Если это будет производная нечетногопорядка, n=2m+1, то x₀ есть точка перегиба функции f(x). Если же это будет производная четногопорядка n=2m, то x₀ есть точка локального экстремума функции f(x).