Свойства операции дифференцирования.

1. ;

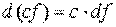2. ;

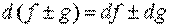3. ;

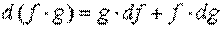4. ;

5. .

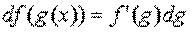Дифференциалы высших порядков.

Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка. Дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка. Вообще, дифференциалом n-го порядка называется дифференциал от дифференциала n -1-го порядка. Имеют место следующие формулы:

.

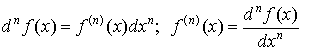Формула Тейлора

Пусть функция f(x) имеет в точке x₀ все производные до n-го порядка включительно. Тогда ее можно представить в виде

).

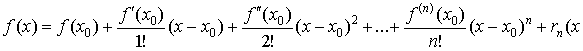Эта формула носит название формулы Тейлора и она является одной из важнейших формул математического анализа. Слагаемое 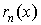называется остаточным членом. Записанная в виде

она называется рядом Тейлора.

Остаточный член в форме Пеаноимеет вид 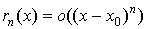. Практического значения эта формула не имеет, но очень полезна пр теоретическом исследовании.

Остаточный член в форме Лагранжаимеет вид

,

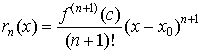где x₀< c< x. Она используется для количественной оценки погрешности представления функции f(x) формулой Тейлора.