Производные высших порядков

Производная от производной первого порядка называется производной второго порядка. Производная от производной второго порядка называется производной третьего порядка. Вообще, производной n-го порядка называется производная от производной n -1-го порядка. По определению сама функция считается производной нулевого порядка от самой себя.

; ; ... , . .

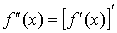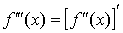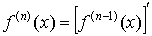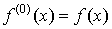Относительно этих производных надо знать формулу Лейбница

.

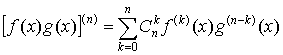Дифференциал

Определение.Функция f(x) называется дифференцируемой в точкех, если ее приращение 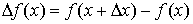может быть представлено в виде

.

Линейная часть приращения функции, то есть слагаемое 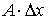называется дифференциаломфункции в точке х и обозначается так: .

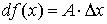Теорема. Для того, чтобы функция f(x) была дифференцируемой в точкех, необходимо и достаточно, чтобы она имела производную в этой точке. При этом 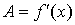, 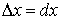и .

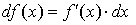Геометрический смысл дифференциала изображен на рис. 3.5. Заметьте, что производная есть отношениедифференциала функции к дифференциалу независимой переменной:

.

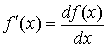Это – самая обычная дробь.

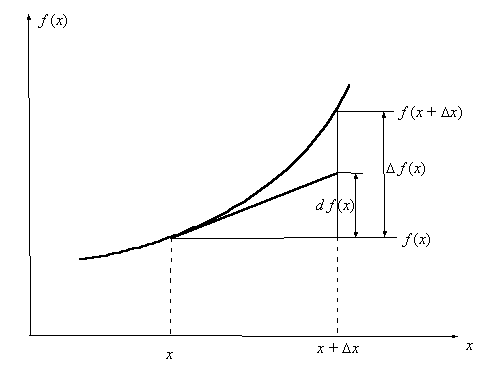
Рис. 3.5 Геометрический смысл дифференциала.