Односторонние производные

Определение производной

Пусть функция f(x) непрерывна в точке x. Тогда производной 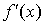от этой функции в точке x, называется предел (разумеется, если он существует)

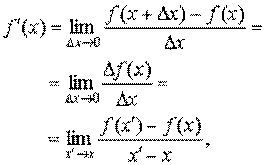
где 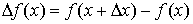- приращение функции.

Геометрический смысл производной состоит в том, что численно она равна тангенсу угла между касательной, проведенной к кривой в точке x, и осью абсцисс OX (см. рис. 3.1).

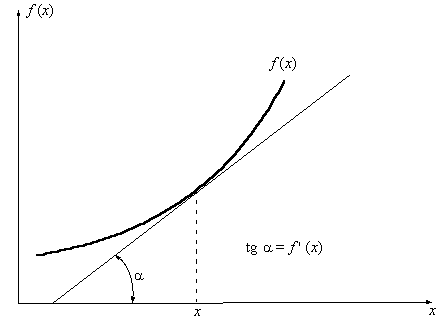
Рис. 3.1 Геометрический смысл производной.

Правила вычисления производных (алгебра производных)

Ниже приводятся основные формулы, служащие для вычисления производных.

1. ;

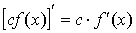2. ;

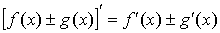3. ;

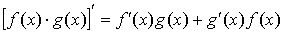4. ;

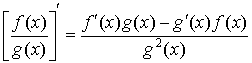5. ;

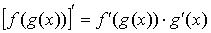6. .

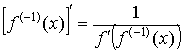Таблица производных

Ниже приводится таблица производных от элементарных функций, которую надо знать так же хорошо, как таблицу умножения.

Функция	Производная	Функция	Производная
с		ctg x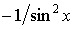
xm	mxm-1	arc sin x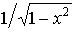
ax	ax×ln a	arc cos x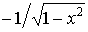
ex	ex	arc tg x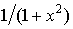
logax		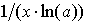arc ctg x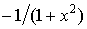
ln x		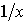sh x	ch x
sin x	cos x	ch x	sh x
cos x	- sin x	th x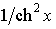
tg x		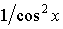cth x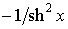

Односторонние производные

Выражение

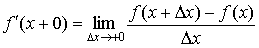
называется производной справафункции f(x) в точке x. Аналогично, выражение

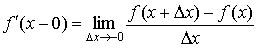
называется производной слевав этой же точке.

Если 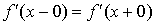, то в точке x существует 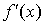; если же 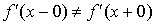, то в точке x производной 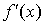не существует и график функции имеет излом; в этой точке имеется две касательных (см. рис. 3.2).

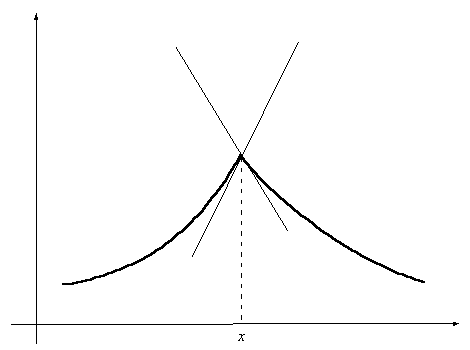
Рис. 3.2 Вид графика функции в окрестности точки,

в которой односторонние производные не равны друг другу.