Разложение в ряд Тейлора некоторых функций

Ниже приводятся самые популярные разложения в ряд Тейлора.

1. ;

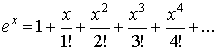2. ;

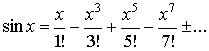3. ;

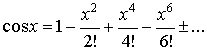4.

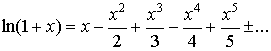
5. .

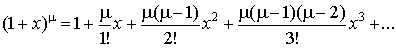При целой степени последняя формула превращается в так называемый бином Ньютона

,

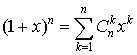где - биномиальный коэффициент .

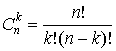Правило Лопиталя

Правило Лопиталя используется для раскрытия неопределенностей типа 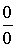и .

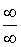Теорема 1.Пусть f(x) и g(x)

1. определены в (a, b);

2. ;

3. в (a, b) существуют 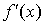и 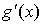, причем ;

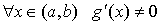4. существует .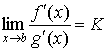

Тогда существует и .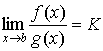

Теорема 2.Пусть f(x) и g(x)

1. определены в (a, b);

2. ;

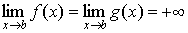3. в (a, b) существуют 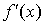и 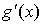, причем ;

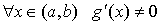4. существует .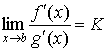

Тогда существует и .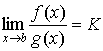

Заметьте, что b может быть равно +¥.

Короче говоря, правило Лопиталя утверждает, что предел отношения функций равен пределу отношения их производных.

Связь производной и монотонности функции

Теорема.Пусть f(x) определена и непрерывна на промежутке 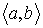и внутри него имеет конечную производную. Для того, чтобы f(x) монотонно возрастала (убывала), необходимо и достаточно, чтобы было ( ).

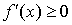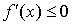Экстремумы функции

Определение.Говорят, что функция f(x) имеет в точке x₀ локальный максимум (минимум) если

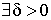такое, что .

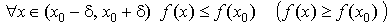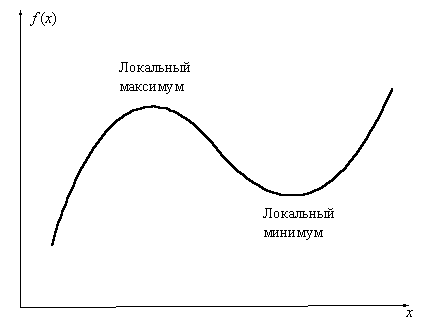
Рис. 3.6 Вид локальных максимума и минимума

Приблизительный вид локального максимума и локального минимума приведен на рис. 3.6. Оба эти термина объединяют термином локальный экстремум.

Необходимое условие экстремумадается теоремой Ферма. Если во внутренней точке x₀ функция f(x) имеет локальный экстремум, то в ней .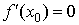

Достаточное условие экстремума.Пусть в точке x₀ выполнено условие 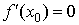. Найдем первую по порядку старшинства производную, отличную от нуля: 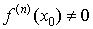. Тогда возможны следующие варианты.

а) n=2m – четное число. Тогда в точке x₀ имеет место локальный экстремум, причем если 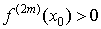, то в точке x₀ – локальный максимум, а если 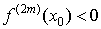, то в точке x₀ – локальный минимум.

б) n=2m+1 – нечетное число. Тогда в точке x₀ локального экстремума нет (это – точка перегиба).