II. Множества и операции над ними.
Цель:
обучения:
– обеспечить усвоение студентами понятий: множество, подмножество, элемент множества, характеристическое свойство элементов множества, равные множества, не пересекающиеся множества, пересечение множеств, объединение множеств, вычитание множеств, дополнение множества, законы пересечения и объединения множеств, классификация, разбиение множества на классы, декартово произведение множеств, кортеж, комбинаторика.
– добиться усвоения студентами:
ü что любое множество можно задать одним из двух способов;
ü математического языка обозначений;
ü правила разбиения множества на классы;
ü правила нахождения числа элементов в объединении конечных множеств;
ü правила нахождения числа элементов в разности конечных множеств;
ü правила нахождения числа элементов в декартовом произведении конечных множеств;
ü правил комбинаторики (суммы и произведения).
– отработать навык:
ü наглядного изображения отношений между множествами – кругами Эйлера;
ü выполнения преобразований, используя свойства коммутативности, ассоциативности и дистрибутивности;
ü наглядного представления декартова произведения множеств;
ü использования правил комбинаторики.
развития:
– развитие аналитико-синтезирующего мышления: умение классифицировать факты, делать обобщающие выводы;
– развитие познавательных умений: вести конспект;
– развитие коммуникативно-технических умений: нешаблонно, творчески подходить к решению самых разнообразных задач;
– развитие умения работать в должном темпе;
воспитания:
– формирование мотивов учения, положительного отношения к знаниям;
– воспитание эстетических взглядов.
2.1. Понятия множества.
Множество – совокупность объектов, обозначается прописными буквами латинского алфавита: A, B, C, . . . , Z.
Элементы множества – объекты, из которых образовано множество, обозначаются строчными буквами латинского алфавита: a, b, c, . . . , z.
 элемент
элемент
принадлежит множеству: 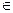
| не принадлежит множеству: 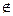
| ||
| Пример: М – множество точек окружности К – множество точек круга | Пример: Запишите с помощью знаков 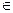 и и 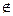 , какие из отрезков AB, CD, EF и PH проходят через точку М, а какие через неё не проходят. , какие из отрезков AB, CD, EF и PH проходят через точку М, а какие через неё не проходят.
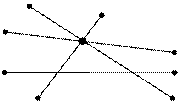 P B
C
D
M
E F
A H P B
C
D
M
E F
A H
| ||
 В •
• А
• О
• F • С В •
• А
• О
• F • С
| 
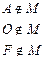
| 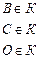
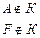
| |



 множество
множество
| пустое | с одним элементом | конечное | бесконечное |
| не имеет элементов, обозначается Ø | состоит из одного элемента | ü множество цифр; ü множество месяцев в году. | ü множество натуральных чисел; ü количество звёзд на небе. |
Числовые множества:
N – натуральные числа;
Z – целые числа;
Q – рациональные числа;
R – действительные числа.
2.2. Способы задания множеств.
 способы задания множеств
способы задания множеств
| перечисление всех элементов множества (для конечных множеств с небольшим количеством элементов) | указание характеристического свойства элементов (для бесконечных множеств и множеств с большим количеством элементов) | |
Пример:
а) множество цифр: 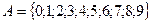 ; ;
| ||
б) множество натуральных чисел, меньших 11:
В = 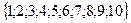 = {b | b = {b | b 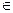 N и b < 11} N и b < 11}
| ||
| перечислили все элементы | указали характеристическое свойство элементов | |
в) множество действительных чисел, больше или равных – 15,6: 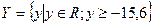
| ||
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
2.3. Операции над множествами.
Наглядно отношения между множествами изображают при помощи особых чертежей, называемых кругами Эйлера.
| I | Множество В называется подмножествоммножества А, если каждый элемент множества В является также элементом множества А, следовательно
Ø пустое множество является подмножеством любого множества, т.е. Ø 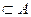 ;
Ø любое множество является подмножеством самого себя, т.е. ;
Ø любое множество является подмножеством самого себя, т.е. 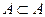 . .
| 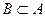 «В – подмножество А»
«В включается в А»
«В – подмножество А»
«В включается в А»

|
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 68: № 1. | ||
| II | Множества А и В называются равными, если 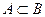 и и 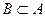 , следовательно
Ø равные множества состоят из одних и тех же элементов;
Ø порядок записи элементов множества не существен. , следовательно
Ø равные множества состоят из одних и тех же элементов;
Ø порядок записи элементов множества не существен.
|  А = В
А = В
|
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 68: № 2. | ||
| III | Пересечениеммножеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А и множеству В, т.е.
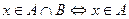 и и 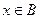
|
  
|
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 72: № 6; 7; 8; 10. | ||
| IV |  Множества А и В не пересекаются, если они не имеют общих элементов, т.е. их пересечение пусто, т.е.
если А ∩ В = Ø, то А ∩ В Множества А и В не пересекаются, если они не имеют общих элементов, т.е. их пересечение пусто, т.е.
если А ∩ В = Ø, то А ∩ В
| А ∩ В |
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 68: № 6 (1; 2; 4). | ||
| V | Объединениеммножеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А или множеству В, т.е.
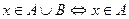 или или 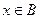
|  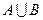
|
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 74: № 6; 7; 10. | ||
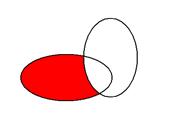
| VI | Пусть 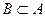 . Дополнениеммножества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В, т.е.
если . Дополнениеммножества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В, т.е.
если 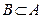 , то В′А = , то В′А = 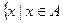 , но , но 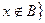
|  
|
| VII | Пусть 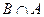 . Разностьюмножеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В, т.е.
если . Разностьюмножеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В, т.е.
если 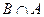 , то , то 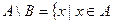 , но , но 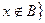
| А В А\В |
| Пример: Л.П. Стойлова, А.М. Пышкало, «Основы начального курса математики». стр. 79: № 3; 11. |
2.4. Понятие разбиения множества на классы.
Классификация – это распределение объектов по классам на основании сходств объектов внутри класса и их отличия от объектов других классов.
Пример:
а) математика:
- натуральные числа: чётные и нечётные;
- углы на плоскости: прямые, острые и тупые.
- и т.п.
б) биология: классификация животных;
в) ботаника: классификация растений.
Множество Х разбито на классы Х1, Х2, . . . , Хп, если:
1. подмножества Х1, Х2, . . . , Хп попарно не пересекаются (т.е. не имеют общих элементов);
2. объединение подмножеств Х1, Х2, . . . , Хп совпадает с множеством Х (т.е. 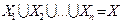 ).
).
Пример: множество учащихся школы разбито на классы:
1. один тот же ученик не может одновременно обучаться в разных классах;
2. объединив учащихся всех классов получим учеников всей школы.
Замечание: если не выполнено хотя бы одно из условий, классификацию (разбиение множества на классы) считают неправильной.
Пример:
 Рассмотрим множество натуральных чисел N. Нас интересуют числа, обладающие свойством «быть кратным 3» - это свойство позволяет выполнить разбиение множества N на два класса (подмножества):
Рассмотрим множество натуральных чисел N. Нас интересуют числа, обладающие свойством «быть кратным 3» - это свойство позволяет выполнить разбиение множества N на два класса (подмножества):
– числа, кратные 3; N
– числа не кратные 3.
Выделенные подмножества не пересекаются,
а их объединение совпадает с множеством N.
Замечание: если на множестве Х задано одно свойство,
то это множество разбивается на два класса:
первый – это класс объектов, обладающих этим свойством;
второй – дополнение первого класса до множества Х (такая классификация называется дихотомической – от греческого dichotomia – сечение на две части).
Пример:
 Рассмотрим множество натуральных чисел N. Разобьём его на классы «числа, кранные 3» и «числа, кратные 5».
Рассмотрим множество натуральных чисел N. Разобьём его на классы «числа, кранные 3» и «числа, кратные 5».

 А – подмножество чисел, кратных 3; А В
А – подмножество чисел, кратных 3; А В
В – подмножество чисел, кратных 5;N
I – подмножествочисел, кратных 3 и 5;I
II – подмножество чисел, кратных 3 и не кратных 5;
III – подмножество чисел, кратных 5 и не кратных 3;
IV – подмножество чисел, не кратных 3 и не кратных 5. IV
2.5. Задачи, связанные с операциями над конечными множествами .
Пусть число элементов конечного множества А будет обозначено символом п(А).
Например, если 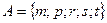 , то можно записать, что п(А)=5, и сказать, что в множестве А содержится 5 элементов.
, то можно записать, что п(А)=5, и сказать, что в множестве А содержится 5 элементов.
Пример:
Пусть даны множества: 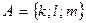 и
и 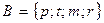
Имеем: п(А)=3, п(В)=4 и 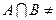 Ø
Ø
Получаем: 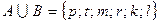 , следовательно
, следовательно 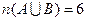 .
.
Дата добавления: 2016-02-16; просмотров: 5219;
