Формулы для подсчёта числа элементов

1. если заданы конечные множества А и В, такие, что 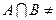Ø, то

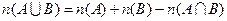
2. если заданы конечные множества А и В, такие, ч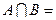то Ø, то

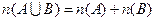
3. если заданы конечные множества А и В, такие, ч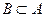то , то

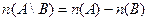
Пример:

а) «Из 32 учащихся класса 21 посещают школьную библиотеку, 13 – городскую библиотеку, 5 учащихся – и школьную и городскую библиотеки. Есть ли в классе учащиеся, которые не посещают ни школьную, ни городскую библиотеку?»

решение:

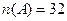– всего учащихся в классе;

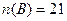– учащиеся, посещающие школьную библиотеку;

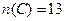– учащиеся, посещающие городскую библиотеку;

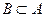и 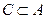(подмножества множества А) и 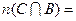5.

Изобразим описанную ситуацию при помощи кругов Эйлера:

Выделение двух подмножеств В и С привело к разбиению множества А на четыре класса: Ø учащиеся, которые посещают и школьную и городскую библиотеки (5 чел.); Ø учащиеся, которые посещают школьную библиотеку и не посещают городскую библиотеку (21 – 5 = 16 чел.); Ø учащиеся, которые посещают городскую и не посещают школьную библиотеку (13 – 5 = 8 чел.); Ø учащиеся, которые не посещают ни школьную, ни городскую библиотеку.

Чтобы ответить на вопрос задачи надо из общего числа учащихся класса вычесть число учащихся множества 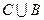. Найти 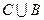можно различными способами:

Ø просуммировать число учащихся, оказавшихся в первых трёх классах: 16 + 5 + 8 = 29;

Ø воспользоваться формулой .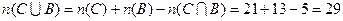

Получаем, 32 – 29 = 3 – учащиеся, которые не посещают ни школьную, ни городскую библиотеку.

(лекция 6)