Нахождение неизвестного

	сложение		вычитание
а + в = с	1слагаемое + 2слагаемое = сумма	а – в = с	уменьшаемое – вычитаемое = разность
а = с – в	1слагаемое = сумма – 2слагаемое	а = с + в	уменьшаемое = разность + вычитаемое
в = с – а	2слагаемое = сумма – 1слагаемое	в = а – с	вычитаемое = уменьшаемое – разность
	умножение		деление
а × в = с	1множитель × 2множитель = произведение	а : в = с	делимое : делитель = частное
а = с : в	1множитель = произведение : 2множитель	а = с × в	делимое = частное × делитель
в = с : а	2множитель = произведение : 1множитель	в = а : с	делитель = делимое : частное

Два уравнения называются равносильными, если множества их корней совпадают.

Пример:

х² – 9 = 0 х² = 9 х₁ = 3 х₂ = – 3 Ответ: 3 и – 3	–13(2х + 6)(х – 3) = 0
2х + 6 = 0 или 2х = – 6 х₁ = – 3 Ответ: 3 и – 3	х – 3 = 0 х₂ = 3

Вывод: данные уравнения равносильны.

Произведение равно нулю тогда и только тогда, когда хотя бы из множителей равен нулю, т.е. 15 × 129 × (− 50) × 7х × 38 × 0 × 63,27 × 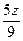× × 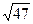56492 = 0

Теоремы равносильности:

Теорема 1: Если к обеим частям уравнения прибавить одно и то же выражение с переменной (имеющее смысл), то получим новое уравнение равносильное данному, т.е. если дано уравнение f(x) = g(x), то ему равносильным будет уравнение f(x) + h(x) = g(x) + h(x).

Следствие 1: Если к обеим частям уравнения прибавить одно и то же число, то получим уравнение, равносильное данному.

Следствие 2: Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части уравнения в другую, поменяв при этом знак слагаемого на противоположный, то получим уравнение, равносильное данному.

Теорема 2: Если обе части уравнения умножить (или разделить) на одно и то же выражение (имеющее смысл и не обращающееся в нуль), то получим новое уравнение, равносильное данному, т.е. если дано уравнение f(x) = g(x), то ему равносильным будет уравнение f(x) × h(x) = g(x) × h(x).

Следствие: Если обе части уравнения умножить (или разделить) на одно и то же число (не равное нулю), то получим уравнение, равносильное данному.

Модуль (абсолютная величина) числа – расстояние от точки, изображающей это число на координатной прямой, до начала отсчёта (нуля), т.е.

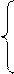| – 4 | = | 4 |

в,

если в > 0

|в| =

если в = 0

– 4 0 4

– в,

если в < 0

Пример:

а) (х – 4,5)(х + 9) = 0 левая часть уравнения – произведение, равное нулю, следовательно,	б) \|х – 1\| = 5,3 по определению модуля
х – 1 = 5,3 х = 5,3 + 1 х₁ = 6,3	– (х – 1) = 5,3 – х + 1 = 5,3 – х = 5,3 – 1 – х = 4,3 х₂ = – 4,3
х – 4,5 = 0 или х₁ = 4,5	х + 9 = 0 х₂ = – 9
Ответ: 4,5 и – 9	Ответ: 6,3 и – 4,3

1.4 Неравенства с одной переменной.

НЕРАВЕНСТВО	РЕШИТЬ НЕРАВЕНСТВО	РЕШЕНИЕ НЕРАВЕНСТВА
два выражения с переменной, соединённых знаком неравенства	найти множество решений или доказать, что их нет	значение неизвестного, при котором неравенство обращается в истинное числовое неравенство
>; < строгие	≤; ≥ не строгие

Координатная (числовая) прямая – это прямая с заданными на ней:	Чем больше число, тем правее оно расположено на координатной прямой, и наоборот, чем левее число расположено на координатной прямой, тем оно меньше. а в с т
ü положительным направлением; ü началом координат (точка О); ü единичным отрезком (ОЕ).
Число на координатной прямой – координата		а < в < с < т

F O E A R

– 4 0 1 3

О(0), Е(1), А(3), R(6), F(– 4)

<123 4 5 6 7 >

Дата добавления: 2016-02-16; просмотров: 1269;