Выражения. Уравнения. Неравенства.

Цель:

1. обучения:

– обеспечить усвоение студентами понятий: числовое выражение, значение числового выражения, выражение, не имеющее смысла, выражение с переменной (переменными), область определения выражения, тождественно равные выражения, тождество, тождественное преобразование выражения, числовое равенство, числовое неравенство, уравнение с одной переменной, корень уравнения, что значит решить уравнение, равносильные уравнения, теоремы равносильности уравнений, неравенство с одной переменной, решение неравенства, что значит решить неравенство, равносильные неравенства, теоремы равносильности неравенств;

– добиться усвоения студентами, что в основе решения уравнений с одной переменной и неравенств с одной переменной лежит понятие равносильности;

– отработать навык использования теорем равносильности при решении уравнений с одной переменной и неравенств с одной переменной.

2. развития:

– развитие аналитико-синтезирующего мышления: умение классифицировать факты, делать обобщающие выводы;

– развитие познавательных умений: вести конспект;

– развитие коммуникативно-технических умений: нешаблонно, творчески подходить к решению самых разнообразных задач;

– развитие умения работать в должном темпе;

– развитие умений действовать самостоятельно.

3. воспитания:

– формирование мотивов учения, положительного отношения к знаниям;

– воспитание эстетических взглядов.

1.1 Выражения и их тождественные преобразования.

язык
знаковая система, используемая для целей коммуникации и познания
естественный	искусственный
языки общения народов мира (русский, английский, казахский, французский и т.д.)	создаётся и развивается вместе с той или иной наукой (математический и т.д.)

Алфавит математического языка:

1. цифры – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – с их помощью по специальным правилам записываются числа;

2. знаки математических действий (операций) – «+», «–», «×», «:»;

3. знаки математических отношений - 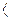, , 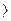≤, ≥, =, ≠ и т.д.;

4. технические знаки – скобки (круглые, квадратные, фигурные и др.);

5. строчные буквы латинского алфавита, их применяют для обозначения чисел.

 

	ВЫРАЖЕНИЕ
	1. числа	1.
	2. знаки математических действий (+, –, ×, :)	2.
числовое	3. круглые скобки	3.	с переменной
	4. степень	4.
	переменная	5.
	значение выражения
единственное	(число, полученное в результате выполнения действий)	множество
числовые выражения, значения которых нельзя найти – не имеют смысла (деление на нуль, квадратный корень из отрицательного числа и т.п.)	множество чисел, при подстановке которых вместо переменной получается числовое выражение, имеющее смысл – область определения выражения или область допустимых значений (ОДЗ)
Пример: а) (27 + 19) × 3 – 49 : 0; б) 148 : (12 – 6 × 2).	Пример: 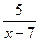= 5 : (х – 7),область определения – все действительные числа, кроме числа 7
			ПОРЯДОК ДЕЙСТВИЙ МОГУТ НАРУШИТЬ ТОЛЬКО СКОБКИ (действия в скобках выполняются первыми, с учётом ступеней)
степень
	I ступень
	«×» и «:»	II ступень
		«+» и «–»

Выражение называют по его последнему действию: указывают порядок действий и последнее действие является названием выражения.

 

Пример: запишите следующие выражения с помощью математиче­ских символов:

а) разность числа 56 и суммы чисел 23 и 4	56 – (23 + 4)
б) сумма разности чисел 56 и 23 и числа 4	(56 – 23) + 4
в) сумма произведения чисел 5 и 7 и разности чисел 71 и 54	5 × 7 + (71 – 54)
г) частное суммы чисел 62 и 2 и разности чисел 35 и 12	(62 + 2) : (35 – 12)
д) произведение частного чисел 63 и 7 и суммы чисел 4 и 8	63 : 7 × (4 + 8)
е) сумма частного чисел 154 и 7 и разности чисел 31 и 9	154 : 7 + (31 – 9)

 

Выражения называются тождественно равными, если при любых значениях переменных из области определения выражений их соответственные значения равны.

Пример: 5(х + 2) и 10 + 5х

	5(х + 2) = 5 × (3 + 2) = 5 × 5 = 25
если х = 3, то
	10 + 5х = 10 + 5×3 = 10 +15 = 25

 

	тождество (равенство)
два тождественно равных выражения соединенных знаком равенства
левая часть = правая часть
5(х + 2) = 5х + 10

 

Пример:

5(х + 2) и (х + 2) × 5– равные выражения 5(х + 2) и 10 + 5х – тождественно равные выражения 5(х + 2) = 5х + 10 – тождество

Тождественное преобразование (равное изменение) – замена выражения другим, тождественно равным ему на некотором множестве.

Тождественные преобразования:

1.	раскрытие скобок 3(5 + 8) = 3×5 + 3×8 = 15 + 24 = 39	распределительный закон умножения   с(а ± в) = са ± св
2.	вынесение общего множителя за скобки 14 − 7х = 2×7 − 7×х = 7(2 − х)
3.	приведение подобных слагаемых	4х − 7 + 6у − 12 − 9х + 5у = −5х − 19 + 11у
4.	взаимное уничтожение противоположных слагаемых	3х − 7 + 5у − 12 − х – 5у – 2х = − 19 (отличаются друг от друга только знаком)
5.	сокращение – деление числителя и знаменателя дроби на одно и то же число (выражение)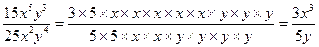
6.	группировка – применение переместительного, сочетательного и распределительного законов для упрощения выражения.
Пример: разложите на множители выражение ах – вх + ав – в2 выполним группировку:
I способ	II способ
ах – вх + ав – в2 = (ах – вх) + (ав – в2) = = х(а – в) + в(а – в) = (а – в)(х + в)	ах + ав – вх – в2 = (ах + ав) – (вх + в2) = = а(х + в) – в(х + в) = (х + в) (а – в)
Вывод: независимо от того, как выполняется группировка, если все тождественные преобразования выполнены верно, то результат будет одинаковым.
7.	и т.д.
ЧИСЛО
простое имеет только два делителя: единицу и само себя Пример:	составное имеет больше двух делителей Пример:
а) 3 = 3 × 1; б) 13 = 13 × 1; в) 23 = 23 × 1;	г) 47 = 47 × 1; д) 53 = 53 × 1; е)	а) 4 = 1× 2 × 2; б) 15 = 1 × 3 × 5; в) 21 = 1 × 3 × 7;	г) 48 = 1 × 2 × 2 × 2 × 2 × 3; д) 51 = 1 × 3 × 17; е) 125 = 1× 5 × 5 × 5.

1.2 Числовые равенства и неравенства.

ЧИСЛОВЫЕ
равенства			неравенства
два числовых выражения соединённых знаком
равенства (=) Пример: а) 3 + 2 = 6 – 1 (и), т.к. 5 = 5 б) 3 + 2 = 7 – 3 (л), т.к. 5 ≠ 4	неравенства (<; >; ≥; ≤) Пример: а) 6 + 2 > 13 – 7 (и), т.к. 8 > 6 б) 6 + 2 ≤ 13 – 7 (л), т.к. 8 > 6
Числовые равенства (неравенства) могут быть как истинными, так и ложными.
Свойства:
1. если к обеим частям истинного числового равенства (неравенства) прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство (неравенство);
2. если обе части истинного числового
равенства умножить на одно и то же числовое выражение, имеющее смысл, то получится истинное числовое равенство.	неравенства умножить на одно и то же числовое выражение, имеющее смысл и
положительное значение - отрицательное значение, а также поменять знак неравенства на противоположный
то получится истинное числовое неравенство.
Пример: 5 = 5 (и) а) 3 + 2 = 6 – 1 | × 2 2 × (3 + 2) = 2 × (6 – 1) 10 = 10 (и)	5 = 5 (и) б) 3 + 2 = 6 – 1 | × ( – 2) –2 × (3 + 2)= –2 × (6 – 1) – 10 = – 10 (и)	Пример: 8 > 6 (и) а) 6 + 2 > 13 – 7 | × 3 3 × (6 + 2) > 3 × (13 – 7) 24 > 18 (и)	8 > 6 (и) б) 6 + 2 > 13 – 7 | × (– 3) – 3 × (6 + 2) < – 3 × (13 – 7) – 24 < – 18 (и)

 

Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.

 

(практика 1)

1.3 Уравнения с одной переменной.

УРАВНЕНИЕ		РЕШИТЬ УРАВНЕНИЕ		КОРЕНЬ УРАВНЕНИЯ
равенство, содержащее неизвестное (высказывательная форма или предиката)		найти все его корни или доказать, что их нет		значение неизвестного, при котором уравнение обращается в верное числовое равенство