Предельный переход.
Найдем теперь предел
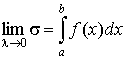 .
.
Определение.Если существует 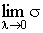 и он не зависит от
и он не зависит от
а) способа разбиения отрезка 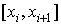 на части и от
на части и от
б) способа выбора средней точки,
то говорят, что 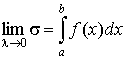 есть определенный интегралот функции f(x) по отрезку [a, b].
есть определенный интегралот функции f(x) по отрезку [a, b].
Функция f(x) называется в этом случае интегрируемойна отрезке [a, b]. Величины a и b называются нижним и верхним пределами интегрирования соответственно.
Суммы Дарбу. Классы интегрируемых функций
Пусть 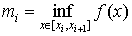 и
и 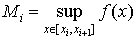 . Составим суммы
. Составим суммы
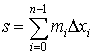 и
и 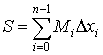 .
.
Они называются суммами Дарбу.
Тогда верна следующая
Теорема.Для существования определенного интеграла необходимо и достаточно, чтобы 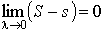 .
.
Эта теорема позволяет установить классы интегрируемых функций.
Теорема 1.Если f(x) ограничена на [a, b] и имеет на нем лишь конечное число точек разрыва, то она интегрируема на [a, b].
Теорема 2.Если f(x) монотонна и ограничена на [a, b], то она интегрируема на [a, b].
Свойства определенных интегралов
Ниже перечислены основные свойства определенного интеграла.
1. 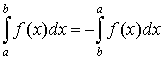 ;
;
2. если 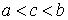 , то
, то 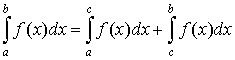 ;
;
3. 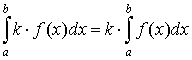 ;
;
4. 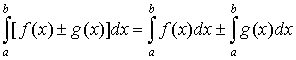 ;
;
5. 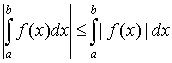 ;
;
6. если 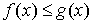 , то
, то 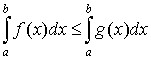 .
.
Дата добавления: 2016-04-06; просмотров: 686;
