Магнитное упорядочение и магнитный фазовый переход.

Ферро-, антиферро- и ферримагнетики отличаются от парамагнетиков тем, что в этих случаях в образце существует магнитное упорядочение даже в отсутствии внешнего магнитного поля. Причем в ферромагнетиках и ферримагнетиках может наблюдаться так называемая спонтанная намагниченность (СН). Естественно, что для существования СН требуется, чтобы атомы, составляющие кристалл, обладали ненулевыми магнитными моментами. Это могут быть атомы (ионы) с частично заполненными 3d, 4f, 5f оболочками. Ориентация магнитных моментов атомов в кристалле может быть параллельной - ферромагнетики (рис.1а) или антипараллельной в антиферромагнетиках (рис.1б) и ферримагнетиках (рис.1в).

Рис.1

Встает вопрос о силах, которые заставляют ориентироваться магнитные моменты атомов в кристалле. На первый взгляд, это могут быть силы магнитного диполь-дипольного взаимодействия. Оценим энергию такого взаимодействия:

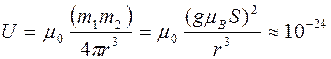Дж » 0,1 К. (1)

В формуле (1):

≈ 1,256•10^-6 Гн/м - магнитная постоянная;

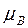≈ 9,27•10^-24 Дж/Тл - магнетон Бора;

S - спин атома;

g - множитель Ланде; 1 < g < 2;

r - расстояние между атомами, r ≈ 2·10^-10 м.

Оценка показывает, что энергия такого магнитно-дипольного взаимодействия очень мала, и оно может быть эффективным только при сверхнизких ( ≈ 0,1К) температурах. Однако из практики известно, что многие вещества обладают спонтанной намагниченностью при температурах очень высоких - до 1000К. Ясно, что магнитное упорядочение в них не может быть обусловлено дипольным взаимодействием.

Энергии, равные 10^-20 – 10^-21 Дж имеют электростатические взаимодействия между электронами в атоме. Эти взаимодействия отвечают за корреляцию электронных спинов в атоме, а в кристалле они же отвечают за корреляцию спинов во всем объеме кристалла и называются обменными взаимодействиями:

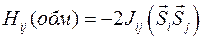, (2)

где 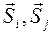- спины i-го и j -го атомов; 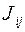- т.н. «обменный интеграл».

Задачу теоретического вычисления обменных интегралов нельзя к настоящему времени считать решенной, поэтому величи­ну 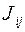рассматривают обычно как некую полуэмпирическую конс­танту, которую можно определить опытным путем. Для этого величину 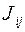необходимо связать с какими-то макроскопически­ми параметрами вещества, определяемыми в опытном порядке.

Энергию обменного взаимодействия для i-го атома, взаимодействующего со всеми атомами кристалла, можно получить, просуммировав по всем j-ым атомам:

. (3)

Здесь мы предполагаем, что в образце реализуется ферромагнитное упорядочение всех спинов, поэтому опускаем знак скалярного произведения векторов. Преобразуем это выражение:

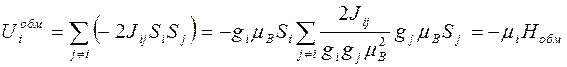, (4)

где через мы обозначили магнитный момент i-го атома, а второй сомножитель мы обозначили через Н_обм - так называемое обменное поле (молекулярное поле, поле Вейсса).

Следует еще раз подчеркнуть, что обменное поле не является магнитным полем. Происхождение обменных сил электростатическое. Но, проведя преобразование (4), мы свели задачу отыскания намагниченности магнитоупорядоченного вещества к известной задаче отыскания намагниченности парамагнетика, только вместо внешнего поля на магнитный момент i-го атома действует теперь обменное поле.

Предположив, что 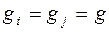и 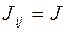одинаковы для любой пары атомов, для Н_обм получим:

. (5)

Если теперь учитывать обменные взаимодействия i-го атома только с ближайшими z соседними атомами, а такое допущение справедливо, т.к. обменное взаимодействие экспоненциально убывает с расстоянием, то

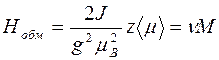, (6)

где М - намагниченность кристалла;

ν - множитель Вейсса.

Для намагниченности кристалла, состоящего из N атомов, можно записать

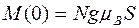(7)

Это выражение будет справедливым при Т = 0, а при конечной температуре его надо умножить на В_S(х)

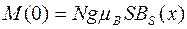, (8)

где В_S(х) –функция Бриллюэна:

;

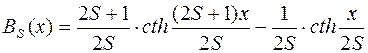Формула 8 аналогична формуле для намагниченности парамагнетика, но для парамагнетика числитель аргумента функции Бриллюэна представлял энергию магнитного момента во внешнем поле, а для ферромагнетика в числителе стоит сумма внешнего и обменного полей.

При Т ® 0, B_S (х) ®1 и мы получаем максимальное значение намагниченности. С ростом температуры тепловые движения атомов приводят к нарушению коллинеарности их магнитных моментов, намагниченность уменьшается до тех пор, пока вещество не станет парамагнитным при температуре Кюри T_С. Величину Н_обм можно оценить из соотношения:

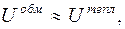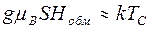т.е. . (9)

В высокотемпературной области, когда kT становится боль­ше, чем 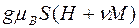, разлагая в ряд функцию Бриллюэна, получим для намагниченности:

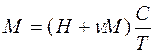, (10)

где 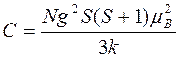- постоянная Кюри.

Магнитная восприимчивость, равная отношению намаг­ниченности к полю, вызвавшему эту намагниченность, запишется как:

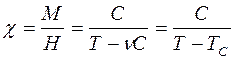, (11)

где Т_С - температура Кюри

. (12)

Значит, по экспериментально измеренной температуре Кюри можно определить обменный интеграл (если, конечно, известна структура вещества, т.е. число z).