Амплитудно – фазовый метод измерения толщины диэлектрических покрытий на электропроводящих основаниях

В ряде случаев при проведении измерений толщины покрытий представляет интерес использование в качестве информативных параметров амплитуды и фазы напряжения ∆Ů, позволяющих при определенных условиях измерять толщину многослойных покрытий или снижать влияние мешающих факторов.

Амплитудно-фазовый метод объединяет в себе достоинства обоих выше описанных методов. Главным отличием амплитудно-фазового метода от амплитудного и фазового заключается в том, что все параметры сигнала рассматриваются как информативные.

На рис. 2.16 изображены годографы изменения вектора напряжения ∆Ů при изменении толщины слоев двухслойного покрытия.

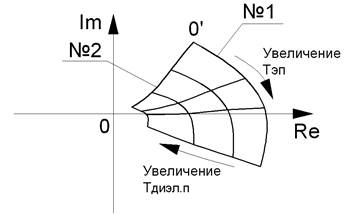
Рис. 2.16. Годографы изменения вектора разностного напряжения ∆Ů при изменении толщины слоев двухслойного покрытия на ферромагнитном электропроводящем основании.

При изменении толщины нижнего слоя – электропроводящего покрытия, конец вектора ∆Ů преимущественно поворачивается по или против часовой стрелки, при этом изменяется его фаза, амплитуда уменьшается незначительно. Вектор напряжения ∆Ů описывает дугу годографа №1, на рис. 2.16. При увеличении толщины верхнего слоя – диэлектрического покрытия (зазора), преимущественно уменьшается длина вектора ∆Ů, а его фаза практически не изменяется. Вектор напряжения ∆Ů описывает дугу годографа № 2, на рис. 2.16. При комбинации изменения толщины как нижнего слоя – электропроводящего покрытия, так и верхнего – диэлектрического покрытия, соответствующие линии годографа смещаются либо приближаясь к точке 0, при увеличении толщины диэлектрического покрытия, либо поворачиваясь вокруг точки 0, при изменении толщины нижнего слоя – электропроводящего покрытия.

Следует учитывать, что линии годографов изменения толщины наружного слоя диэлектрического покрытия – не прямые линии. Это означает, что не существует однозначной зависимости фазы вектора ∆Ů от толщины нижнего слоя и для однозначного его определения необходимо учитывать оба нелинейных параметра, и амплитуду, и фазу. Пример такой «двумерной» градуировочной характеристики представлен на рис. 2.17. Поскольку измерение амплитуды и фазы, с точки зрения схемотехники, являются разноплановыми задачами, могут возникать ошибки результатов измерений. Для уменьшения ошибок производится переход от полярной системы координат (амплитуда и фаза) к декартовой прямоугольной (реальная и мнимая часть сигнала).

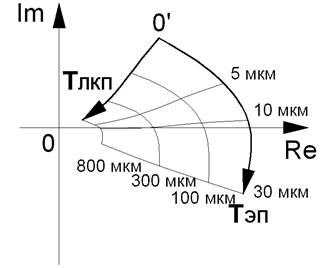
Рис. 2.17. Пример градуировочной характеристики вихретокового амплитудно-фазового метода измерения толщины двухслойного покрытия (Основание – ферромагнитная сталь, нижний слой – цинк, верхний слой – лакокрасочное покрытие)

Аналогично может производится измерение толщины двухслойных покрытий и на неферромагнитном основании. На рис. 2.18 изображены годографы изменения вектора напряжения ∆Ů при изменении толщины слоев двухслойного покрытия. Первый слой – серебро гальваническое, нанесенное на основание из алюминиевого сплава с подслоем меди, второй слой – прозрачный лак. Такая комбинация используется для изготовления рекламной и имиджевой продукции («серебряные» визитки, визитницы и пр. аксессуары). Поскольку электропроводности меди и серебра очень близки, измеряется их суммарная толщина.

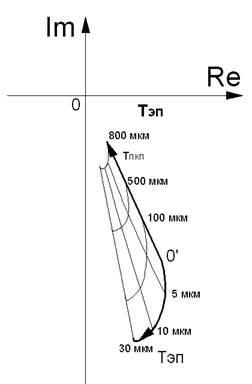
Рис. 2.18. Годографы изменения вектора напряжения ∆Ů при изменении толщины слоев двухслойного покрытия на неферромагнитном электропроводящем основании

При использовании амплитудно-фазового метода возможны и другие комбинации оснований и измеряемых покрытий.

На основаниии вышесказанного можно выделить три возможных метода вихретокового вида контроля с использованием многообмоточных первичных измерительных преобразователей, применимых для построения толщиномеров защитных покрытий:

- амплитудный метод, основанный на амплитуды разностного напряжения преобразователя (применим для измерения толщины защитных диэлектрических покрытий на неферро- и ферромагнитных основаниях);

- фазовый метод, основанный на изменении фазы разностного напряжения преобразователя (применим для измерения толщины электропроводящих ферро- и неферромагнитных покрытий на электропроаводящих ферро- и неферромагнитных основаниях, в различном сочетании, с возможностью отстройки от влияния некоторых мешающих факторов, измерения толщины листовых электропроводящих неферромагнитных материалов);

- амплитудно – фазовый метод, основанный на изменении амплитуды и фазы разностного напряжения преобразователя (применим, например, для одновременного послойного раздельного (независимого) измерения толщины диэлектрического покрытия, нанесенного на электропроводящее неферромагнитное покрытие, в свою очередь нанесенное на электропроводящее ферромагнитное основание, листовых электропроводящих неферромагнитых материалов, электропроводящих ферро- и неферромагнитных покрытий на диэлектрических основаниях)

Недостатками выше перечисленных методов являются необходимость изготовления с высокой точностью нескольких обмоток, а также сложность функциональных преобразований для определения первичных информативных параметров. В связи с этим представляет интерес использование абсолютных параметрических однообмоточных измерительных преобразователей для решения ряда задач измерения толщины покрытий.

Построение векторной диаграммы однообмоточного измерительного преобразователя. Частотный метод измерения толщины диэлектрических и электропроводящих покрытий на электропроводящих основаниях

Рассмотрим структурную электрическую схему абсолютного параметрического однообмоточного измерительного преобразователя без ферромагнитных сердечника и экрана (рис. 2.19).

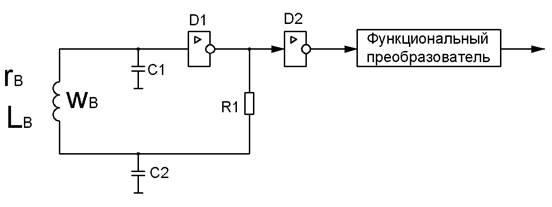
Рис. 2.19. Структурная электрическая схема абсолютного параметрического измерительного преобразователя без ферромагнитных сердечника и экрана.

Обмотка возбуждения W_в с активным сопротивлением провода r_в включена в колебательный контур, состоящий из конденсаторов C₁ и C₂. В качестве активного элемента выступает инвертор D1. Резистор r₁ обеспечивает коэффициент обратной связи К_ос>1, что необходимо для работы колебательного контура, и, одновременно, образуя с конденсатором C₂ низкочастотный RC фильтр, производит фильтрацию сигнала с выхода инвертора D1 , представляющего собой меандр. Инвертор D2 выполняет функции развязывающего элемента (буфера), отделяющего колебательный контур от влияния последующих элементов схемы.

Данная схема является развитием схемы генератора Колпитца. Частота колебаний контура определяется по формуле:

____

f = 1/[2p(Ö(L_вC_е)), (2.7.1)

где C_е = C₁C₂/(C₁+ C₂).

Следует обратить внимание, что частота колебаний контура не зависит от активного сопротивления обмотки.

Поскольку представленная выше схема работает по принципу колебательного контура, то для описания работы преобразователя и построения векторных диаграмм целесообразно использовать не векторы токов, напряжений и вносимых напряжений, а активные и реактивные сопротивления обмотки возбуждения, а также их изменения.

Векторная диаграмма комплексного сопротивления (импеданса) обмотки возбуждения в функции изменения зазора h^*, представлена на рис. 2.20, а.

а)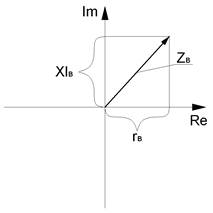

б) 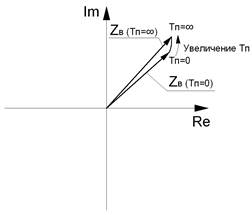в)

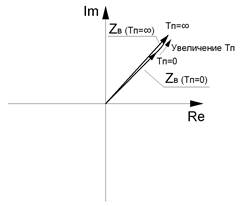
Рис. 2.20. Векторная диаграмма абсолютного частотного (параметрического) измерительного преобразователя:

а - преобразователь не взаимодействует с объектом контроля (h^*= Т_п = ∞), б - преобразователь над неферромагнитном электропроводящим полупространством (h^*= Т_п = 0), в - преобразователь над ферромагнитном электропроводящим полупространством (h^*= Т_п = 0).

Витки обмотки W_в сцеплены с магнитным потоком самоиндукции, который индуцирует в обмотке ЭДС самоиндукции, направленную противофазно току İ_в обмотки возбуждения. Реактивное сопротивление обмотки Xl_в зависит от круговой частоты и индуктивности Xl_в=wL_в.

При установке преобразователя над неферромагнитным электропроводящим объектом (полупространством) вихревые токи индуцируют в обмотке возбуждения W_в ЭДС взаимоиндукции. ЭДС взаимоиндукции имеет фазовый сдвиг незначительно больший 180° относительно İ_в. Как следствие, реактивное и активное сопротивления обмотки уменьшаются. При этом конец вектора опишет дугу, являющуюся годографом вносимого импеданса (рис. 2.20, б). Чем выше частота колебаний контура, тем более вытянутой будет дуга.

При установке преобразователя над ферромагнитным электропроводящим объектом (полупространством) к описанным выше эффектам добавится эффект увеличения индуктивного сопротивления Xl_в (рис. 2.20, в).

Поскольку измеряемым параметром, как и в случае использования амплитудного метода, является расстояние от преобразователя до поверхности электропроводящего объекта контроля (зазор h^* или толщина диэлектрического покрытия Т_п), а мешающими параметрами – его электропроводность и магнитная проницаемость, то характеристики преобразователя и его схемы выбираются такими, чтобы значение обобщенного параметра b было как можно большим для уменьшения их влияния на результат измерения. Оптимальным можно считать значение обобщенного параметра b в пределах 60…200.

В зависимости от параметров преобразователя (радиус обмотки, сопротивление провода, площадь сечения провода) и от условий контроля (частота возбуждения, электропроводность и магнитная проницаемость материала объекта контроля), значение параметров обмотки (активное и реактивное сопротивления) при установке преобразователя на ферромагнитный или неферромагнитный объект контроля будет различным (рис. 2.21).

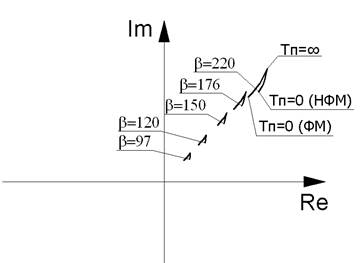
Рис. 2.21. Годографы изменения импеданса абсолютного частотного (параметрического) однообмоточного измерительного преобразователя, установленого над неферромагнитным (НФМ) и над ферромагнитным (ФМ) электропроводящим полупространством при различных частотах возбуждения

При увеличении частоты возбуждения преобразователя (без взаимодействия с объектом контроля) увеличивается как индуктивное сопротивление Xl_в, так и активное r_в сопротивление обмотки. Изменение активного сопротивления связано с возрастанием влияния скин-эффекта в проводах обмотки. Это приводит к вытеснению тока в проводах обмотки к их поверхностному слою и, как следствие, уменьшению эффективной площади сечения провода. Так же при увеличении частоты (обобщенного параметра b) наблюдается уменьшение влияния магнитной проницаемости на сигналы с преобразователя.

С помощью абсолютного параметрического однообмоточного измерительного преобразователя и частотной схемы его подключения возможно измерение толщины не только диэлектрических покрытий, но и электропроводящих неферромагнитных покрытий на электропроводящем неферромагнитном основании. Возможность измерения объясняется на рис. 2.22. Электропроводящее неферромагнитное покрытие толщиной Т_п , электропроводностью s_п, нанесенное на неферромагнитное электропроводящее основание электропроводностью s_осн в зоне вихревых токов. Вихревые токи, индуцированные в объекте контроля, распространяются как в слое покрытия, так и в слое основания. Вихревые токи в каждом слое оказывают свое, различное друг от друга влияние на результирующее магнитное поле системы преобразователь-объект контроля.

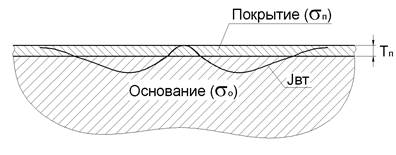
Рис. 2.22 . Распространение вихревых токов в электропроводящем неферромагнитном покрытии и электропроводящем неферромагнитном основании

Можно говорить о некоторых интегральном значении электропроводности s_и объекта контроля в объеме распространения вихревых токов, изменяющихся в зависимости от толщины покрытия Т_п. Так, если толщина покрытия Т_п=0, то интегральная электропроводность и объекта контроля в зоне вихревых токов будет равна s_осн. При увеличении толщины покрытия до значения Т_п=¥, интегральная электропроводность объекта контроля будет равна s_П. Если электропроводности основания и покрытия различны, то при увеличении толщины покрытия будет изменяться ЭДС взаимоиндукции (амплитуда и фаза) и, соответственно, будет изменяться импеданс обмотки (индуктивное сопротивление Xl_в и активное r_в сопротивление обмотки), что приведет к изменению частоты f колебательного контура. Таким образом, значение частоты f колебательного контура будет зависеть от толщины покрытия.

Бесконечной толщине покрытия, в случае вихретокового контроля, будет соответствовать максимальная глубина проникновения вихревого тока, равная Т_¥=2pd.

Для обеспечения приемлемой чувствительности следует выбирать условия контроля таким образом, чтобы значение обобщенного параметра b было относительно невелико (»60). Для измерения толщины электропроводящих неферромагнитных покрытий на электропроводящих неферромагнитных основаниях важно чтобы соблюдались следующие соотношения их электропроводности: s_П/s_осн > 2 или s_П/s_осн < 0,6.

На основании вышеизложенного можно выделить частотный (параметрический) метод вихретокового вида контроля с использованием однообмоточных первичных измерительных преобразователей для построения толщиномеров диэлектрических защитных покрытий на электропроводящих неферро- и ферромагнитных основаниях, а также электропроводящих неферромагнитных покрытий на электропроводящих неферромагнитных основаниях.

Преимущества однообмоточного частотного (параметрического) преобразователя и описанной выше схемы:

- возможность изготовления преобразователей с высоким значением обобщенного параметра b, недостижимого для трансформаторных преобразователей, реализующих амплитудный, фазовый и амплитудно-фазовый метод. Как следствие, возможно изготовление высокочастотных преобразователей с малой глубиной проникновения вихревого тока;

- простота конструкции и схемы подключения.