Предельный признак сравнения.
Пусть даны два знакоположительных ряда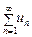 
(1) и 
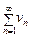(2). Если существует конечный, отличный от 0 предел 
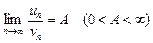, то ряды (1) и (2) сходятся или расходятся одновременно.
Пример 8. Исследовать на сходимость ряд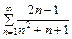 
.
Решение
Исследуемый ряд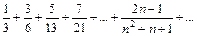 
.
1. Проверим выполнение необходимого признака
.
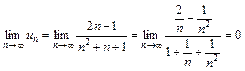2. Ряд с положительными членами.
3. Применим предельный признак сравнения. Для того, чтобы догадаться, с каким рядом целесообразно сравнить данный ряд, рассмотрим его общий член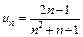 
. Для больших значений n числитель можно считать приближенно равным 2n, a знаменатель - 
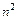. Поэтому 
.
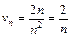Вычислим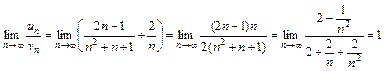 
.
Ряд с общим членом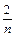 
является гармоническим, который всегда расходится, то и данный ряд расходящийся.
Признак Даламбера.
Пусть дан ряд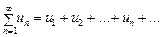 
с положительными членами и существует конечный или бесконечный предел 
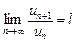. Тогда ряд сходится при 
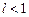и расходится при 
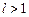.Пример 9. Исследовать на сходимость ряд 
.
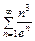Решение
Исследуемый ряд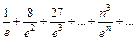 
.
1. Необходимый признак выполняется
,
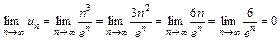здесь неопределенность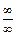 
, поэтому трижды применяем правило Лопиталя.
2. Ряд с положительными членами.
3. Применим к данному ряду признак Даламбера: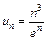 
, 
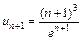, вычислим предел отношения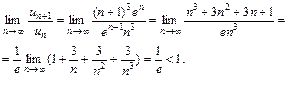 
Ряд сходится.
Пример 10. Исследовать на сходимость ряд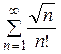 
.
Решение
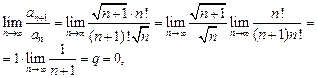
следовательно, исследуемый ряд сходится.
Пример 11. Исследовать на сходимость ряд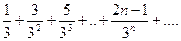 
Решение
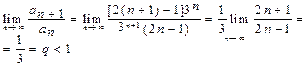, следовательно, ряд сходится.
Признак Коши.
Есл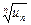и 
при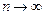 
стремится к определенному числу q, то при q<1 ряд 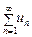с положительными членами сходится; при q> он расходится.
Пример 12. Исследовать на сходимость ряд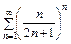 
.
Решение
Исследуемый ряд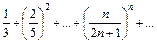 
.
1. Необходимый признак выполняется, действительно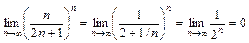 
.
2. Ряд с положительными членами.
3. Общий член ряда находится в n-ой степени, в таких случаях удобно пользоваться признаком Коши
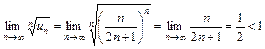. Ряд сходится.
Пример 13. Исследовать на сходимость ряд 
.
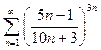Решение
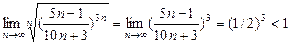, следовательно, ряд расходится. ●
Дата добавления: 2016-02-13; просмотров: 1044;