Интегрирование выражений вида .
Разложение правильной рациональной дроби
В сумму простейших дробей.
Пусть дана правильная дробь: 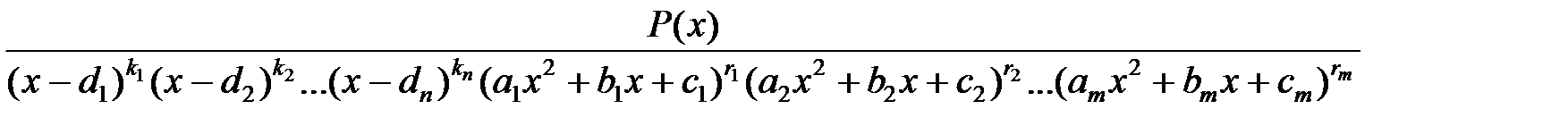 Тогда каждому множителю
Тогда каждому множителю 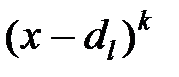 соответствует сумма простейших дробей
соответствует сумма простейших дробей  , а каждому множителю вида
, а каждому множителю вида 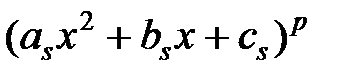 соответствует сумма простейших дробей
соответствует сумма простейших дробей 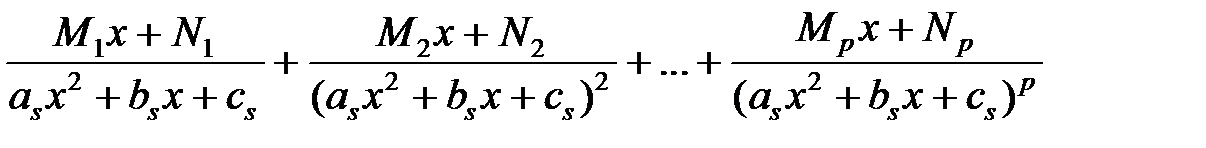
Примеры.
1. Найти вид разложения рациональной дроби на сумму простейших дробей: 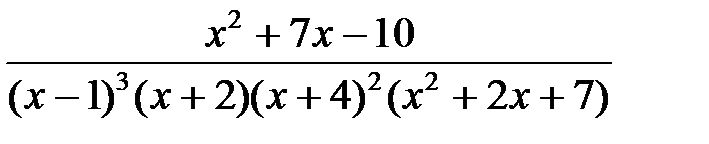 .
.
Решение: 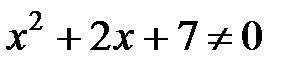 , так как
, так как 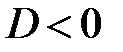 Þ на линейные множители разложить нельзя.
Þ на линейные множители разложить нельзя. 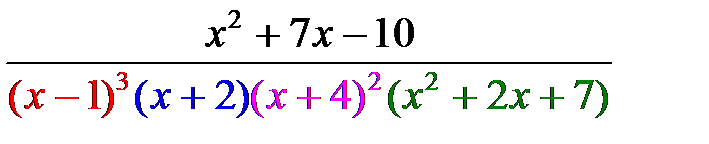 =
= 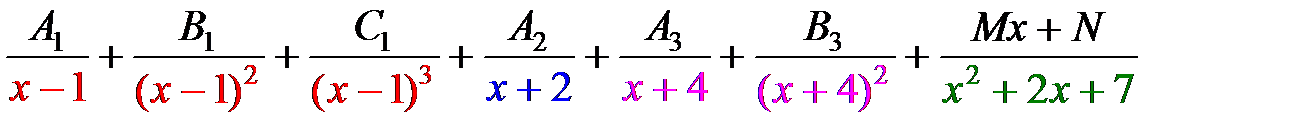
2. Найти 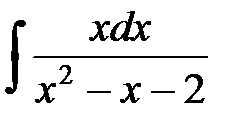 .
.
Решение. 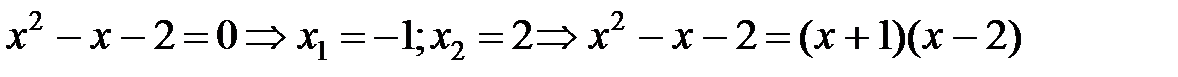 .
.
Разложим рациональную дробь на сумму простейших дробей:
 при
при 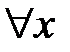 . Найдем коэффициенты A и B. Так как знаменатели равны, приравняем числители:
. Найдем коэффициенты A и B. Так как знаменатели равны, приравняем числители: 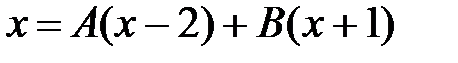 .
.
При 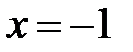 получим:
получим: 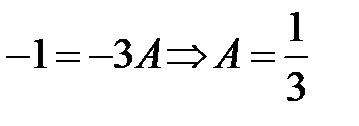 . При
. При 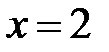 получим:
получим: 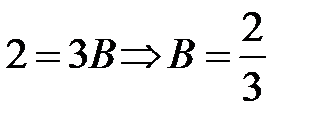 . Следовательно,
. Следовательно,  Þ
Þ 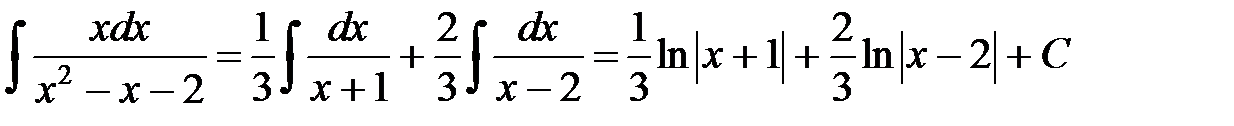 .
.
3. Найти 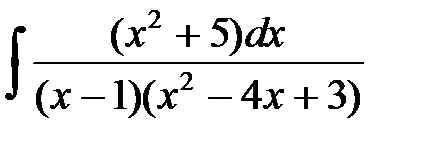 .
.
Решение. 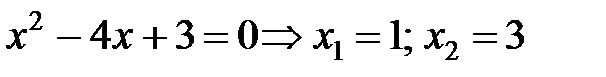 Þ
Þ 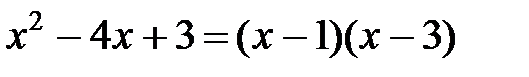 . Дробь правильная. Разложим на сумму простейших:
. Дробь правильная. Разложим на сумму простейших: 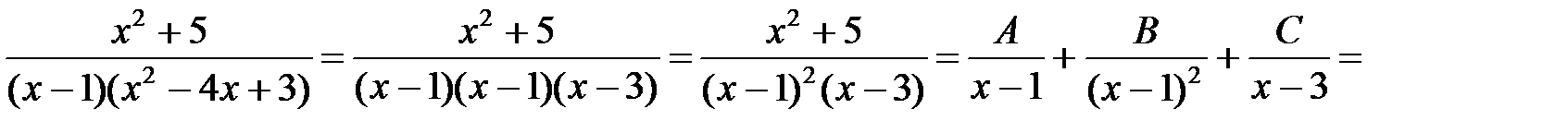
 . Верно при
. Верно при 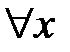 . Приравниваем числители:
. Приравниваем числители: 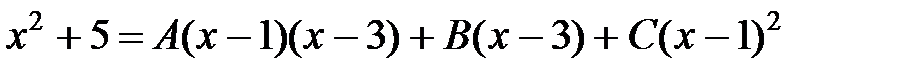 . Найдем
. Найдем 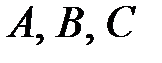 .
.
При 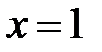 имеем:
имеем: 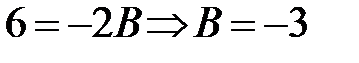 . При
. При 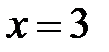 получим:
получим:  .
.
При 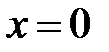 получим:
получим: 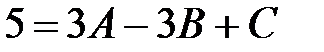 ;
; 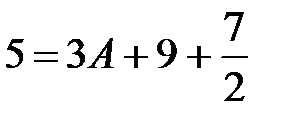 Þ
Þ 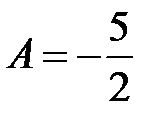 . Следовательно,
. Следовательно,
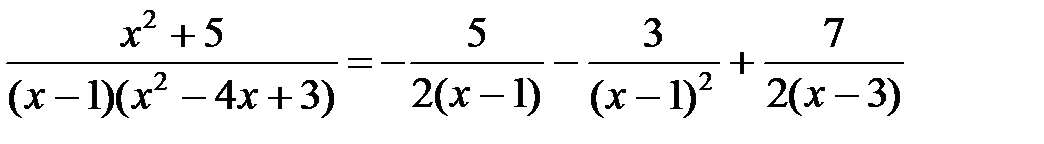 .
. 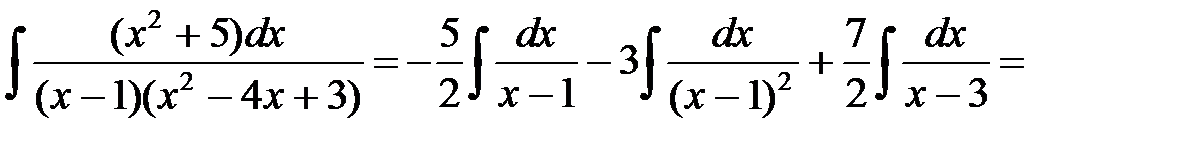
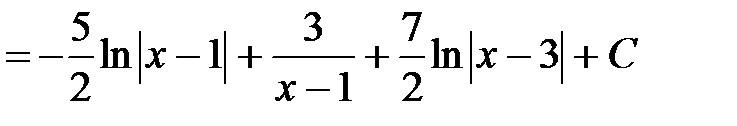 .
.
(Так как 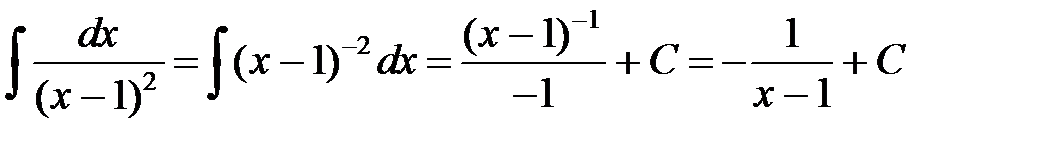 ).
).
4. Найти 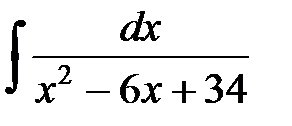 .
.
Решение. Уравнение  не имеет действительных корней Þ выражение
не имеет действительных корней Þ выражение 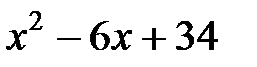 нельзя разложить на множители. Преобразуем:
нельзя разложить на множители. Преобразуем:
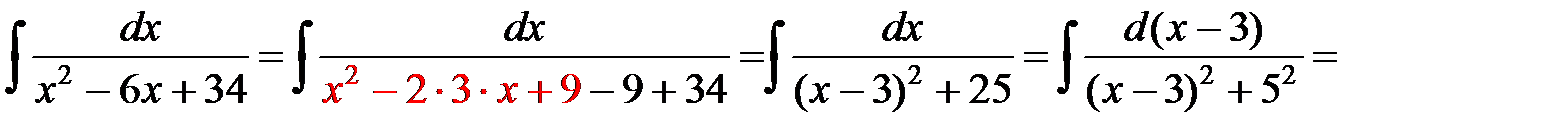
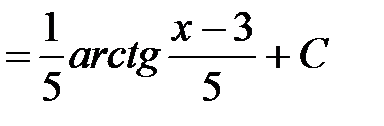 .
.
Интегрирование выражений вида .
Интегралы 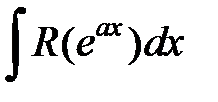 при помощи подстановки
при помощи подстановки  можно свести к интегралам
можно свести к интегралам 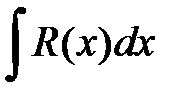 , которые мы рассматривали ранее.
, которые мы рассматривали ранее.
Пример. Найти 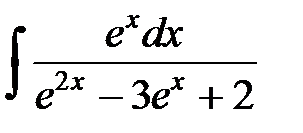 .
.
Решение. Сделаем замену переменной: 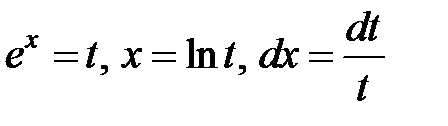 . Тогда
. Тогда 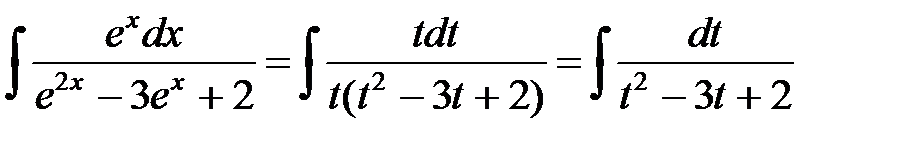 . Разложим на сумму простейших дробей:
. Разложим на сумму простейших дробей: 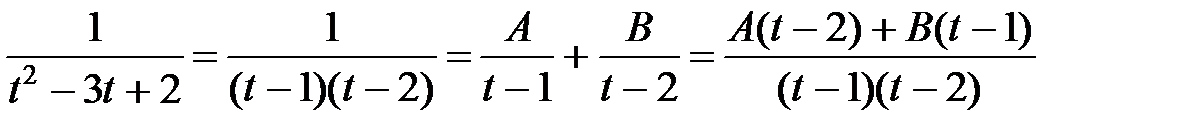 Þ
Þ  . При
. При 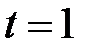 :
: 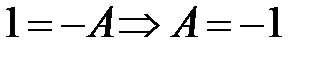 . При
. При 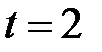 :
: 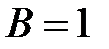 .
. 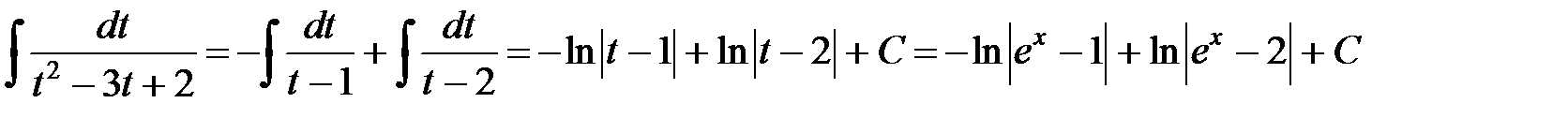
Интегралы вида  , где
, где 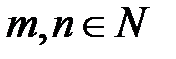 .
.
1. Если m нечетное, то 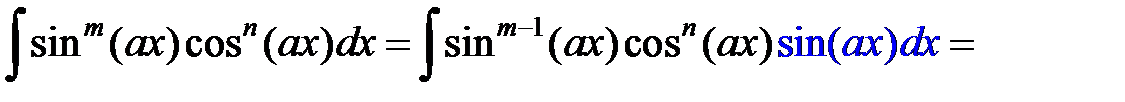
 , делаем замену
, делаем замену 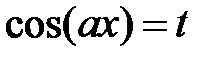 . Так как m-1 –четное, то
. Так как m-1 –четное, то 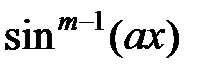 выражаем через
выражаем через 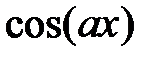 .
.
2. Если n нечетное, то 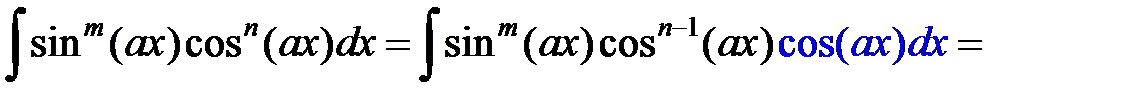
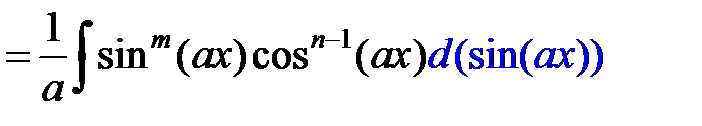 .
.
3. Если оба числа m и n- четные, то используем формулы понижения степени:
 ;
; 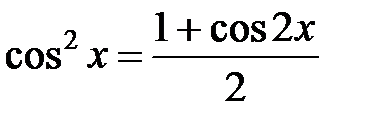 .
.
Примеры.
1. 

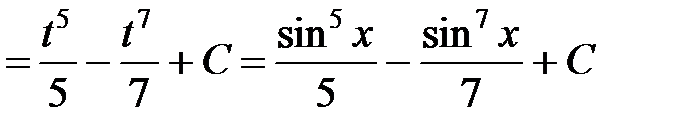 .
.
2. 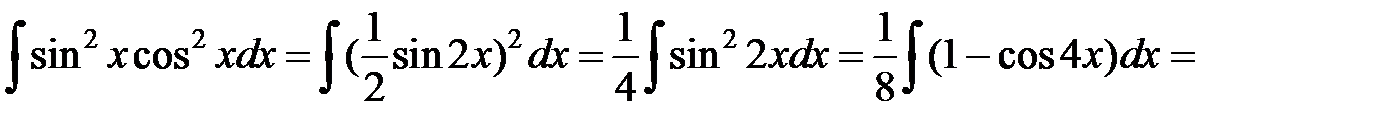
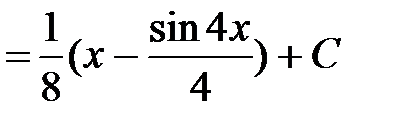 .
.
Интегралы вида 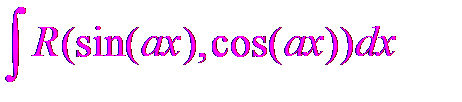
Метод основан на формулах: 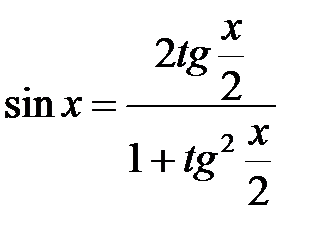 ,
, 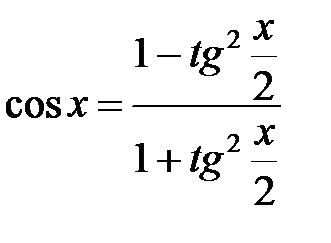 . Произведя замену переменной:
. Произведя замену переменной: 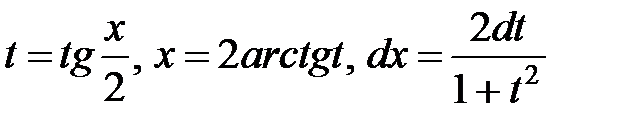 , мы придем к
, мы придем к 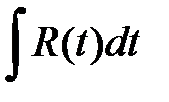 , который можем найти.
, который можем найти.
Пример. 
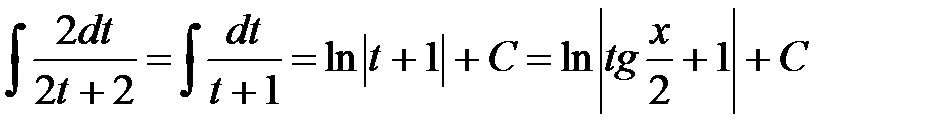 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Понятие рационального потребителя. Равновесие потребителя и правило максимизации полезности. |
Дата добавления: 2016-04-22; просмотров: 814;
