Унификация. Метод резолюций в логике предикатов

Перенесем метод резолюций в логику предикатов. Основная идея здесь принадлежит математику Эрбрану.

Определение 10.6.Две литеры l 1= Р ( x ), l 2= Р ( y ) называются унифицируемыми , если существуют такие подстановки свободных переменных, при которых литеры совпадут:

l 1= l 2= Р ( a ) при х = а , у = а .

Пример 10.10. Применим правило резолюции к резольвентной паре 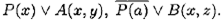Тогда будем иметь резольвенту А (а , у ) ∨ В ( a , z ). Это записывают следующим образом:

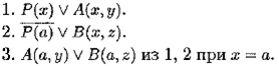
Большое неудобство для применения метода резолюций в логике предикатов связано с наличием кванторов. Для преодоления этой трудности разработаны два приема. Один назван в честь математика Сколема — исключение по Сколему всех кванторов существования , другой — вынос всех кванторов общности за скобки .

Определение 10.7.Пусть имеются формулы с кванторами существования:

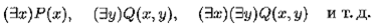
Тогда исключение по Сколему кванторов существования проводится следующим образом:

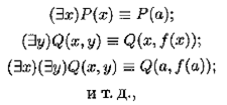
где a , f ( x ) — неизвестные постоянная и функция, называемые сколемовскими .

Вывод . Метод резолюций состоит в следующем:

1) задача — доказать общезначимость формулы F ;

2) перейти к формуле 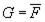и сделать тесное отрицание в ней;

3) исключить все кванторы существования в G ;

4) вынести все кванторы общности за скобки, предварительно переобозначив связанные переменные с целью различия их от свободных переменных и между собой, получим G = ( ∀ x )( ∀ y ) ... ( ∀ z ) H ;

5) представить формулу H в КНФ, т. е. H = d 1∧ d 1∧ ... ∧ dn, и применить к H метод резолюций с унификацией.

Пример 10.11. Доказать общезначимость формулы логики предикатов

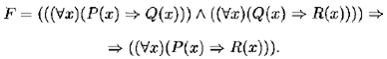
Перейдем к формуле 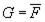сделаем тесное отрицание в G :

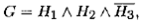
где

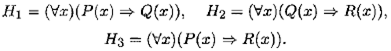
Сделаем тесное отрицание в H 3и исключим квантор существования:

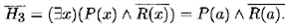
Сделаем замену связанной переменной « x » в Н 2на « y », вынесем все кванторы общности в G за скобки и представим H в КНФ:

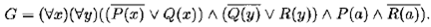
Теперь применим метод резолюций с унификацией, используя стратегию от фактов.

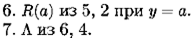
Можно было применить стратегию от цели и запись хорновских дизъюнктов с обратной импликацией.

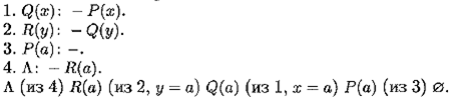
Цит. по: Дискретная математика: учебник для студ. вузов /
Т.С. Соболева, А.В. Чечкин; под ред. А.В. Чечкина. —
М.: Издательский центр «Академия», 2006. — С. 136 – 149. —
(Университетский учебник. Сер. Прикладная математика и информатика).

Тема 4. Алгоритмы