Хорновские дизъюнкты

Дальнейшим упрощением метода резолюций является идея американского математика Хорна использовать только дизъюнкты определенного вида.

Определение 10.5.Дизъюнкт, у которого среди литер не более одной положительной, называется хорновским .

При этом дизъюнкт с одной положительной литерой и наличием отрицательных литер вида

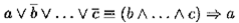
называется правилом и читается так «из b , ..., с следует а ». Дизъюнкт без положительной литеры вида

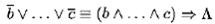
называется целевой дизъюнкт и читается: «из b , ... , с следует ложь».

Наконец, дизъюнкт без отрицательных литер только с одной положительной литерой вида

a ≡ (1 ⇒ a )

называется фактоми читается: «справедливо а ».

Вывод . Для того чтобы доказать методом резолюций, что формула G — тождественно-ложная, рекомендуется выполнить ряд действий.

1. Привести G к КНФ.

2. Преобразовать все дизъюнкты в КНФ в хорновские путем переобозначения некоторых положительных литер в отрицательные.

3. Если все дизъюнкты в КНФ — хорновские, то применение метода резолюций облегчается тем, что всегда можно вести поиск очередной резольвентной пары при помощи одной из следующих двух рекомендуемых стратегий.

Стратегия от фактов.Если среди хорновских дизъюнктов есть факт, т. е. одиночная положительная литера, то надо искать второй дизъюнкт, который составляет с ним резольвентную пару. После применения правила резолюции к такой паре получается резольвента, которая будет короче второго дизъюнкта. При этом если существуют несколько дизъюнктов, парных данному факту, то рекомендуется сначала рассматривать дизъюнкты более короткие. Потом снова ищем факт и к нему короткий парный дизъюнкт и т. д. Получаем множество новых фактов до останова.

Стратегия от цели.Если среди хорновских дизъюнктов есть целевой, т. е. дизъюнкт без положительной литеры, то надо искать второй дизъюнкт, который с ним составляет резольвентную пару. Далее, каждый раз для очередной резольвенты надо искать парный ей дизъюнкт и применять правило резолюций. Получаем дерево подцелей до останова.

Замечание 10.2.Так как решаемая задача в общем алгоритмически неразрешимая, то может случиться, что ни одна из предлагаемых стратегий не приведет к успеху. Тогда надо применять правило резолюций по какой-либо третьей стратегии и т. д.

Пример 10.8. Рассмотрим снова ту же формулу G , что и в предыдущем примере. Только сделаем замену литеры а на литеру 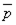, чтобы все дизъюнкты в КНФ для G были хорновские:

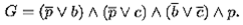
Будем доказывать тождественную ложь формулы G методом резолюций, используя стратегию от фактов. В таком случае исходный факт один — дизъюнкт d 4.

Теперь для сравнения для той же задачи используем стратегию от цели. Целевой дизъюнкт здесь d 3.