Правила преобразования формул логики предикатов

Пусть формулы f и g имеют одно и то же множество свободных переменных (в частности, пустое).

Определение 9.8.Формулы f и g равносильны вданной интерпретацииI = á М , Ф ñ , если на любом наборе значений свободных переменных они принимают одинаковые значения, т. е. если формулы выражают в данной интерпретации один и тот же предикат.

Формулы f и g равносильны намножествеМ , если они равносильны во всех интерпретациях, заданных на множестве М . Формулы f и g равносильны в алгебре (логике) предикатов, если они равносильны во всех интерпретациях. Тогда будем писать: f ≡ g .

Пример 9.6. Рассмотрим формулы:

Эти формулы равносильны на одноэлементном множестве. В самом деле, если область интерпретации — одноэлементное множество, то какой бы предикат ни взяли в качестве интерпретации 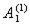на этом множестве, он принимает только значения И или Л.

В первом случае обе формулы принимают значение И, во втором — Л, и, следовательно, они равносильны на этом множестве.

С другой стороны, на двухэлементном множестве {а , b } эти формулы не равносильны.

Теперь рассмотрим правила перехода от одних формул к другим, им равносильным во всех интерпретациях.

Теорема 9.1(правила булевой алгебры ). Для формул алгебры предикатов сохраняются все равносильности и правила равносильных преобразований алгебры высказываний.

Доказательство . Проведем показательное рассуждение для одной равносильности.

Здесь формулы а , b , с являются предикатами. Рассмотрим произвольную интерпретацию I = á М , Ф ñ и зададим свободные переменные в формулах а , b , с конкретными значениями. Тогда эти формулы станут высказываниями со своими истинностными значениями, для которых закон дистрибутивности выполняется. Следовательно, в силу произвольности интерпретации, дистрибутивность будет выполняться в логике предикатов. Аналогично доказываются все равносильности из логики высказываний,

Теорема 9.2(правило переноса квантора через отрицание ). Пусть а — формула, содержащая свободную переменную х . Тогда:

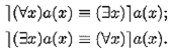
Теорема 9.3(правило выноса квантора за скобки ). Пусть а (х ) содержит свободную переменную х , формула b не содержит переменной х и обе они удовлетворяют п. 3 определения 9.5, т.е. нет таких переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда:

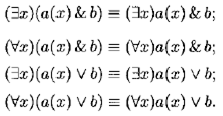
Если в предыдущих правилах допустить, чтобы формула b содержала переменную х , то будут выполняться только две равносильности:

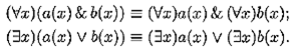
Теорема 9.4(правило перестановки одноименных кванторов ).

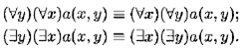
Теорема 9.5(правило переименования связанных переменных ). Заменяя связанную квантором переменную формулы а всюду в области действия квантора другой переменной, не входящей в эту формулу, получаем формулу, равносильную а.

Определение 9.9. Длиной формулыназывается общее число входящих в нее символов предикатов (атомарных формул), логических символов и символов кванторов.

Пример 9.7. Рассмотрим формулу

Эта формула имеет длину 5. Длину здесь составляют символы:

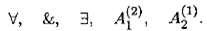
Определение 9.10.Формулы, в которых из логических символов имеются только символы &, ∨ , ⌉ (стандартный базис), причем символ ⌉ встречается только перед атомарными подформулами (тесное отрицание), называются приведенными.

Пример 9.8. Рассмотрим формулы:

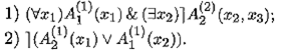
Первая является приведенной, вторая — нет. (Почему?) В заключение укажем, до какой степени формулы можно упростить с помощью равносильностей.

Определение 9.11.Приведенная формула называется нормальной , если она содержит все символы кванторов впереди или кванторов вовсе нет.

Пример 9.9. Формула 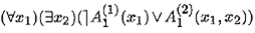является нормальной.

Относительно нормальных формул справедлива следующая теорема, которую приведем без доказательства.

Теорема 9.6.Для любой формулы существует равносильная ей приведенная формула, для которой, в свою очередь, существует равносильная ей нормальная формула.

Пример 9.10. Рассмотрим некоторую теорему из математического анализа.

Теорема Лагранжа о конечном приращении.Если функция f ( x ) непрерывна на отрезке [а , b ] и дифференцируема в интервале (а , b ), то существует точка с , с ∈ (а , b ), такая, что выполняется равенство f ( b ) – f ( a ) = f '( c )( b – а ).

Обратим внимание на то, что классическая математическая символика используется в основном для термов (предметов), а все свойства термов и утверждения о них написаны на естественном языке (см. формулировку теоремы). Математическая логика позволяет формализовать весь текст теоремы и записать ее в виде формулы . Вот почему математическую логику часто называют метаматематикой . Мир формул логики предикатов относят к неклассической математике .

Перейдем к формализации теоремы Лагранжа в рамках логики предикатов.

Шаг 1 . Перечислим все предметы, о которых идет речь в теореме, и обозначим их предметными переменными . Всего в теореме четыре предмета — три числа а , b , с и одна функция f , или в стандартном обозначении f ( x ).

Шаг 2 . Выделим в теореме простейшие части текста (смыслы) о предметах и формализуем их в виде атомарных формул . Получим:

P ( a , b , f ( x )) = «функция f ( x ) непрерывная на отрезке [а , b ]»;

Q ( a , b , f ( x )) = «функция f ( x ) дифференцируемая в интервале (а , b )»;

R (a , b , с ) = « с ∈ ( а , b )»;

S (a , b , с , f (x )) = «f (b ) – f (a )) = f '(c ) (b – а )».

Шаг 3. Соединим атомарные формулы в одну сложную формулу при помощи логических связок, следуя тексту теоремы. Получим следующую формулу рассматриваемой теоремы.