Формулы логики предикатов

Теперь определим понятие формулы логики предикатов.

Определение 9.4. Алфавит логики предикатовсодержит следующие символы.

1. Символы предметных переменных:

x 1, x 2,…

2. Символы предикатов:

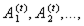
где t = 0, 1,…

3. Логические символы:

⌉, &, ∨ , ⇒ , ~.

4. Символы кванторов:

∃ , ∀ .

5. Скобка и запятая:

), (.

Отличие алфавита логики высказываний от алфавита логики предикатов в наличии п. 1 и 4; кроме того, п. 2 здесь шире (в алфавите логики высказываний t = 0); в п. 5 появилась «запятая».

Чтобы избежать нагромождения индексов, часто символы переменных будем обозначать через x , y , z , а символы предикатов через Р , Q , R , S и т. д.

Определение 9.5.Слово в алфавите логики предикатов называется формулойили правильно построенным словом, если оно удовлетворяет следующему рекурсивному определению.

1. Если 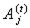— символ предиката; 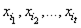— символы предметных переменных, необязательно различные, то 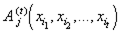— формула. Такая формула называется атомарной. Все предметные переменные атомарных формул свободные, связанных переменных нет.

2. Пусть а — формула. Тогда ⌉ а — тоже формула. Свободные и связанные переменные формулы ⌉ а — соответственно свободные и связанные переменные формулы а .

3. Пусть а и b — формулы, причем нет таких переменных, которые были бы связанными в одной формуле и свободными в другой. Тогда

(а ∨ b ), ( a & b ), (а ⇒ b ), (а ~ b )

есть формулы, в которых свободные переменные формул а и b остаются свободными, связанные остаются связанными.

4. Пусть а — формула, содержащая свободную переменную х . Тогда ( ∀ x )а , ( ∃ х )а — тоже формулы. Переменная x в них — связанная. Остальные переменные, которые в формуле а свободны, остаются свободными и в этих формулах.

Переменные, которые в формуле а связаны, остаются связанными.

В формуле ( ∀ x )а формула а называется областью действияквантора ∀ , а в формуле ( ∃ х )а — областью действия квантора ∃ .

5. Других правил нет.

Замечание 9.2.По определению формулы никакая переменная не может быть одновременно свободной и связанной. Для оценки формулы на истинность и ложность требуется зафиксировать значения всех свободных предметных переменных, взяв их значения из множества допустимых значений.

Пример 9.3 . Рассмотрим предикат «Каждый водитель должен соблюдать правила».

Назовем параметры: «водитель», «правила». Первый параметр — связанная переменная, второй — свободная.

Зафиксируем вторую переменную: «правила дорожного движения». Если такой закон в РФ есть, то получаем «И», если нет, то «Л».

То, что сейчас проделано, называется заданием, или рассмотрением некоторой интерпретации предиката.

Определение 9.6. Интерпретациейназывается пара I = á М , Ф ñ , состоящая из непустого множества М и соответствия Ф. При этом множество М задает область значений предметных переменных, а соответствие Ф сопоставляет каждой атомарной формуле Aj( x 1, ..., xt) конкретный t -местный предикат, заданный на М .

При заданной интерпретации считают, что предметные переменные пробегают множество М, а символы ⌉, &, ∨ , ⇒ , ~.и символы кванторов имеют обычный смысл.

Для данной интерпретации каждая формула без свободных переменных представляет собой высказывание, которое истинно или ложно. Всякая формула со свободными переменными выражает некоторый предикат на множестве М , который истинен при одних значениях переменных из этого множества и ложен при других.

Пример 9. 4. Пусть f ( x ) — произвольная фиксированная функция, заданная на отрезке [а , b ].

1. Рассмотрим интерпретацию I = á М , Ф1ñ , где М — множество действительных чисел; Ф1— соответствие, сопоставляющее формулам Р (х , δ), Q ( x , ε), R (ε) их конкретные предикаты (характеристические функции):

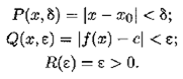
Здесь х 0— фиксированный элемент отрезка [а , b ]; с — некоторое фиксированное действительное число. Тогда определение того, что 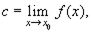записывается формулой

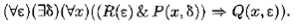
2. Рассмотрим интерпретацию I = á М , Ф2ñ , где М — множество действительных чисел; Ф2— соответствие, сопоставляющее формулам Р (х , δ), S ( x , ε), R (ε) предикаты:

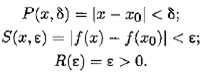
Здесь х 0— произвольный фиксированный элемент отрезка [а , b ]. Тогда определение о том, что функция f ( x ) непрерывна в точке х 0, записывается формулой

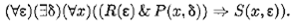
Здесь рассмотрен простой вариант определения формул логики предикатов. Для описания более серьезных языковых конструкций требуется расширение понятия формулы и использование еще понятия терма . Мир термов описывает предметную область интерпретации средствами классической математики. Для определения термов требуется расширить алфавит формальной теории. Кроме символов предметных переменных xiтребуется ввести еще символы констант ajи функциональные символы 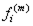алгебраических операций над предметными переменными и над константами. Здесь число m = 0, 1, 2, ... называется арностью или числом мест операции. Терм определяется рекурсивно.

Определение 9.7.Всякая предметная переменная, или константа, является термом .