Программируемые логические матрицы

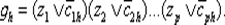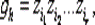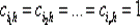Рассмотрим схему, состоящую из р входов z 1, ..., zpи q выходов g 1, …, g q (рис. 6.28), в которой значения выходов определяются матрицей соединений (cih), 1 ≤ i ≤ p , 1 ≤ y ≤ q , cih∈ {0, 1} по следующим правилам Таким образом, где , а остальные cih= 0. Полученная схема называется решеткой с р входами и q выходами элементов &, которая определяется матрицей соединений (cih).

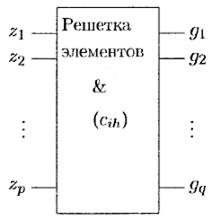
Рис. 6.28

Программируемой логической матрицей (ПЛМ) называется изображенная на рис. 6.29 схема, получающаяся соединением решетки А с 2n входами и k выходами, определяемой матрицей соединений (aih), и решетки В с k входами и т выходами, определяемой матрицей соединений (bhj).

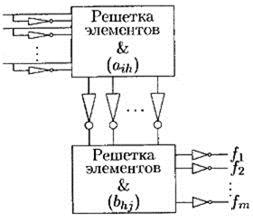
Рис. 6.29

Опишем преобразования, которые происходят при прохождении через ПЛМ значений переменных x 1, x 2, …, xn. Поскольку к каждому входу xiприсоединен инвертор 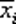, на 2n входов решетки А подаются значения переменных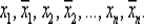

После прохождения решетки A h -й выход принимает значение функции 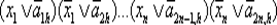, а последующей операции инвертирования соответствует функция

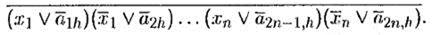
Полученные k значений (1 ≤ h ≤ k ) подаются на входы решетки B , после прохождения которой на выходе j образуется значение функции

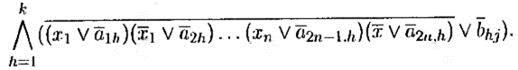
В заключение после инвертирования по законам де Моргана на выходе j получаем значение функции 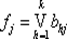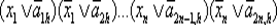, j = 1, …, m . Функции fiсоответствует дизъюнкция конъюнктов (определяемых формулами 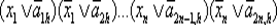) таких, что bhj= 1.

Таким образом, при соответствующем выборе матриц (aih) и (bhj) можно одновременно реализовать m произвольных ДНФ, содержащих не более k различных конъюнктов переменных от x 1, x 2, …, xn.

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов, Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ, 2003. — С. 172–210. — (Серия «Высшее образование»).