Схемы из функциональных элементов

Ориентированная бесконтурная сеть, в которой полюса делятся на входные (входы ) и выходные (выходы ), называется схемой из функциональных элементов . Входные полюса помечаются символами переменных, а каждая вершина, отличная от входного полюса, некоторым функциональным символом. При этом должны выполняться следующие условия:

— если а входной полюс, то полустепень захода вершины а равна нулю: deg ¯(a ) = 0;

— если вершина а не является полюсом и помечена n -местным функциональным символом f , то deg ¯(a ) = п и дуги, входящие в а , перенумерованы от 1 до п .

Функциональным элементом называется всякий подмультиграф схемы, состоящий из невходного полюса а , помеченного соответствующим символом f , и вершины, из которых исходят дуги в вершину а .

Пример 6. 11.1. На рис. 6.25а представлена схема из функциональных элементов. Здесь входные символы помечены символами переменных x 1, x 2, x 3, — одноместный функциональный символ, соответствующий операции отрицания; & — двухместный символ, соответствующий операции конъюнкции, f 3— некоторый двухместный символ, f 1, f 2, f 4— некоторые трехместные символы. Вершины, помеченные символами f 1, f 3, f 4, являются выходными полюсами. Им соответствуют термы: f 1(x 1, x 2, x 3), 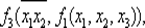f 2(f 1(x 1, x 2, x 3), f 1(x 1, x 2, x 3), x 3)).

На рис. 6.25б изображен функциональный элемент, определяемый вершиной, помеченной символом f 4. Ему соответствует устройство, показанное на рис. 6.25в .

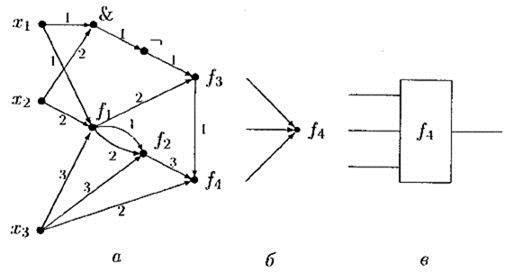
Рис. 6.25

В примере 11.1 продемонстрировано, что каждый вывод схемы порождает некоторый терм.

Говорят, что функция f реализуется схемой ∑, если существует такой выход а схемы ∑, что функция fa, соответствующая терму выхода a , эквивалента функции f .

Схемы из функциональных элементов с одним выходом, у которых входные полюса помечены символами x 1, x 2, …, xn, а вершины, отличные от входных полюсов, — символами ∨ , &, , называются Хп-функциональными схемами . Сложностью схемы из функциональных элементов называется число ее вершин, отличных от входных полюсов. Хп-функциональная схема ∑, реализующая функцию f , называется минимальной , если всякая другая Хп-функциональная схема, реализующая f , имеет сложность, не меньшую, чем сложность схемы ∑.

Сложность минимальной схемы, реализующей функцию f , называется сложностью функции f в классе схем из функциональных элементов и обозначается через L (f ).

Пример 11.2. Сложность функции 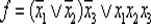совпадает со сложностью Х 3-функциональной схемы, изображенной на рис. 6.26, и равна 8: L (f ) = 8.

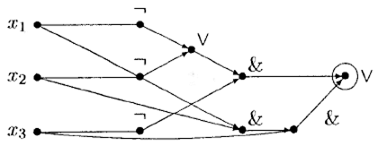
Рис. 6.26

Мультиплексоры

Мультиплексором 2тканалов ( ) называется схема с т + 2твходами у 1, у 2, ..., у m, 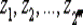и одним выходом g , в которой при у 1= b 1, у 2= b 2, ..., у m= bm, выход g принимает значение 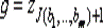, где J (b 1, …, bm) = 20b 1+ 21b 2+ … + 2m– 1bm.

На рис. 6.27 показан мультиплексор MUX 8.

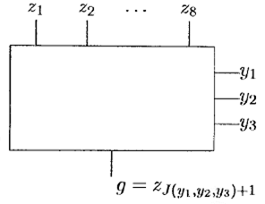
Рис. 6.27

Пример 11.3. Если m = 3, у 1= 1, у 2= 0, у 3= 1; то g = zJ(1, 0, 1) + 1= z 6.

С помощью мультиплексора 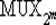, придавая переменным постоянные значения, можно реализовать любую булеву функцию f (у 1, у 2, ..., у m).