Дизъюнктивные и конъюнктивные нормальные формы. Если х — логическая переменная, δ ∈ {0, 1}, то выражение
Если х — логическая переменная, δ ∈ {0, 1}, то выражение
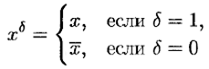
называется литерой . Литеры x и 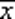 называются контрарными.
называются контрарными.
Элементарной конъюнкцией или конъюнктом называется конъюнкция литер. Элементарной дизъюнкцией или дизъюнктом называется дизъюнкция литер.
Дизъюнкция конъюнктов называется дизъюнктивной нормальной формой (ДНФ); конъюнкция дизъюнктов называется конъюнктивной нормальной формой (КНФ).
Пример 4.2. Формула 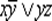 — ДНФ, формула
— ДНФ, формула 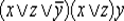 — КНФ, а формула
— КНФ, а формула 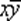 является одновременно КНФ и ДНФ.
является одновременно КНФ и ДНФ.
Теорема 4.1. 1. Любая формула эквивалентна некоторой ДНФ .
2. Любая формула эквивалентна некоторой КНФ .
Опишем алгоритм приведения формулы к ДНФ.
1. Выражаем все логические операции, участвующие в построении формулы, через дизъюнкции, конъюнкции и отрицания, используя эквивалентности (φ → ψ) ~ ( φ ∨ ψ), (φ ↔ ψ) ~ ( φ ∨ ψ) ∧ ( ψ ∨ φ ) и определения операций |, ↓ , и ⊕ .
2. Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания по правилу x ~ x .
3. Используя закон дистрибутивности (φ ∧ (ψ ∨ χ)) ~ ((φ ∧ ψ) ∨ (φ ∧ χ)), преобразуем формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций.
В результате применения пп. 1–3 получается ДНФ данной формулы.
Совершенной ДНФ называется дизъюнкция некоторых конституент единицы, среди которых нет одинаковых, а совершенной КНФ называется конъюнкция некоторых конституент нуля, среди которых нет одинаковых. Таким образом, СДНФ (СКНФ) есть ДНФ (КНФ), в которой в каждый конъюнкт (дизъюнкт) каждая переменная xiиз набора {x 1, x 2, …, xn} входит ровно один раз, причем входит либо сама xi, либо ее отрицание 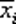 .
.
Для решения задачи нахождения СДНФ и СКНФ, эквивалентных исходной формуле φ , предварительно рассмотрим разложения булевой функции f (x 1, x 2, …, xn) по k переменным (для определенности по x 1, x 2, …, xk) — разложения Шеннона .
Теорема 4.2(первая теорема Шеннона).
Любая булева функция f (x 1, x 2, …, xn) представима в виде разложения Шеннона:
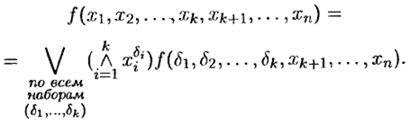
Теорема 4.3 (вторая теорема Шеннона).
Любая булева функция f (x 1, x 2, …, xn) представима в виде разложения Шеннона:
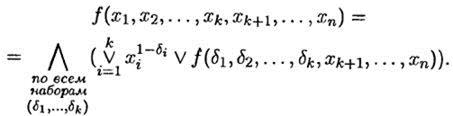
Дата добавления: 2016-02-24; просмотров: 1487;
