Функции алгебры логики

Семантически формулы полностью характеризуются таблицами истинности. При этом можно забыть о синтаксической структуре самих формул и иметь дело с таблицами истинности. Таким образом, мы приходим к понятию функции алгебры логики, которое и будет исследоваться в дальнейшем.

Функцией алгебры логики (ФАЛ) от п переменных (x 1, x 2, …, xn) называется любая функция f : {0, 1}n→ {0, 1}, т. е. функция, которая произвольному набору (δ1, δ2, …, δn) нулей и единиц ставит в соответствие значение f (δ1, δ2, …, δn) ∈ {0, 1}.

Функции алгебры логики называются также булевыми функциями , двоичными функциями и переключательными функциями .

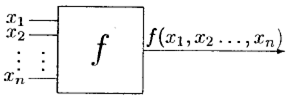
Рис. 6.2

Булевой функцией описываются преобразования некоторым устройством входных сигналов в выходные. Предположим, что устройство, показанное на рис. 6.2, имеет п входов x 1, x 2, …, xn, на которые может подаваться или не подаваться ток, и один выход, на который ток подается или не подается в зависимости от подачи тока на входы. При этом значение переменной xi= 1 интерпретируется как поступление тока на i -й вход, а xi= 0 — как непоступление тока. Значение f (δ1, δ2, …, δn) равно 1, если при x 1= δ1, …, xn= δnток на выход проходит, и f (δ1, δ2, …, δn) = 0, если ток не проходит.

Например, операции конъюнкции x ∧ y соответствует устройство с двумя входами и одним выходом. При этом значение выхода равно 1, тогда и только тогда, когда оба значения входов равны 1 (рис. 6.3).

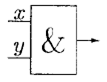
Рис. 6.3

Булева функция f (x 1, x 2, …, xn) полностью определяется своей таблицей истинности :

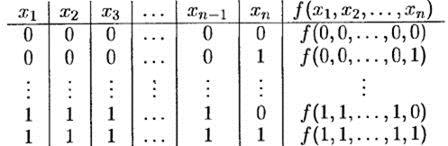
В каждой строке таблицы вначале задается набор значений переменных (δ1, δ2, …, δn), a затем — значение функции на этом наборе.

Если булева функция f и формула φ имеют одну и ту же таблицу истинности, то будем говорить, что формула φ представляет функцию f .

Булева функция также однозначно задается перечислением всех наборов, на которых она принимает значение 0, либо перечислением всех наборов, на которых она принимает значение 1.

Вектором значений булевой функции f (x 1, x 2, …, xn) называется упорядоченный набор всех значений функции f , при котором значения упорядочены по лексикографическому порядку множества аргументов {0, 1}n.

Булева функция f (x 1, x 2, …, xn), принимающая значение 1 (соответственно 0) на всех наборах нулей и единиц: f (x 1, x 2, …, xn) ≡ 1 (соответственно f (x 1, x 2, …, xn) ≡ 0), называется константой 1 (константой 0).