Атомы и шкалы решеток подмножеств

Так как решетки подмножеств это булевы алгебры, то в них можно определить системы образующих и выражать подмножества формулами через такие образующие.

Определение 7.20.Пусть L — решетка подмножеств для X . Элемент а ∈ L называется атомом решетки, если а ≠ ∅ и не существует l ≠ а , l ≠ ∅ , такого, что

∅ ⊂ l ⊂ a .

В решетке L 2рассмотренного примера атомами будут μ1— доктора наук, μ2— кандидаты наук, μ3— без научных степеней. Это самые конкретные понятия решетки. Алгоритм проверки на атомарность — отсутствие более конкретных непустых понятий.

Определение 7.21.Пусть L — решетка подмножеств для X . Тогда подсемейство элементов Ш решетки L называется шкалой решетки, если любой элемент решетки выражается через элементы шкалы Ш с помощью операций пересечения, объединения и разности ( ∩ ,∪ , ).

Итак, в силу того что L имеет алгебраическую структуру, в L можно выбрать систему образующих — шкалу.

Пусть Ш = {ω1,… ω k} — шкала L . Тогда ∀δ ∈ L существует его выражение через элементы шкалы, т. е.

δ = f (ω1,… ω k),

где f — функция алгебры множеств, использующая операции объединения, пересечения, дополнения (разности).

Определение 7.22.Шкала Ш решетки L называется базовой, если ни один из элементов Ш не выражается через другие элементы Ш с помощью операций объединения, пересечения и разности.

Шкала называется атомарнойили разбиением опорного множества, или координатной сеткой, если все ее элементы — атомы.

Базовая шкала в конечной решетке L называется минимальной(максимальной), если в решетке L нет шкалы с меньшим (большим) числом элементов.

Теорема 7.3.Любая решетка имеет хотя бы одну шкалу, например саму решетку.

Теорема 7.4.Решетка подмножеств определяется однозначно любой своей шкалой.

Доказательство . От противного. Пусть существуют две решетки подмножеств L и с одной и той же шкалой Ш.

Тогда для любого элемента λ ∈ L имеем представление его через элементы шкалы с помощью операций объединения, пересечения и разности.

Но в силу того что элементы шкалы Ш принадлежат также и другой решетке , то, производя действия над элементами Ш в соответствии с представлением X , будем получать каждый раз элементы L . Таким образом,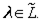

Аналогично доказывается, что элемент 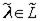принадлежит и решетке L , т. е. решетки L и совпадают.

Теорема 7.5.Пусть L — произвольная решетка для X и L ≠ L 0.

Тогда ее атомарная шкала Шат= {а 1, ..., ап} = Ш mахявляется максимальной шкалой (самой большой, самой неэкономной). Мощность |Шат| = n , | L | = 2п.

Теорема 7.6.Пусть L — конечная решетка для X и L ≠ L 0. Тогда существует

Ш min= {ω1,… ω k}, и число ее элементов k подчиняется равенству:

k = |Ш min| = [ log 2|Ш mах|] + 1,

где [ log 2|Ш mах|] — целая часть числа. Число элементов решетки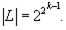

Пример 7.21. Пусть X — времена событий, происходящих в определенные дни недели, и пусть

Шат= {пн, вт, ср, чт, пт, сб, вс}.

Тогда число элементов соответствующей решетки подмножеств | L | = 27.

Найдем Ш minдля L . Число k = [ log 27] + 1 = 3. Следовательно, минимальная шкала

Ш min= {ω1, ω2, ω3}.

Построим эту минимальную шкалу следующим образом. Пронумеруем элементы атомарной шкалы двоичными числами:

пн — 001,

вт — 010,

ср — 011,

чт — 100,

пт — 101,

сб — 110,

вс — 111.

Тогда за ω1возьмем объединение тех атомов, у которых в первом разряде 1, т. е.

ω1= {пн ∪ ср ∪ пт ∪ вс},

далее ω2— объединение тех атомов, у которых во втором разряде 1, и т. д.:

ω2= {вт ∪ ср ∪ сб ∪ вс},

ω3 = {чт ∪ пт ∪ сб ∪ вс}.

Теперь все элементы можно выразить через элементы минимальной шкалы. В самом деле:

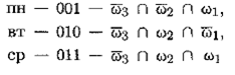
и т. д.

Замечание 7.4. На практике часто выгоднее использовать минимальные шкалы, а не атомарные.

Вывод . Всякая решетка L подмножеств X обладает тремя важными свойствами, которые делают ее одним из основных понятий математической информатики.

• Решетка L — частично упорядоченное множество с отношением включения множеств.

• Решетка L — булева алгебра с тремя операциями: две бинарные операции (объединение и пересечение) и одна унарная операция (дополнение), для которых выполняются аксиомы булевой алгебры.

• Решетка L — топология на опорном множестве X и, следовательно, пара ( X , L ) — топологическое пространство.

Цит. по: Дискретная математика: учебник для студ. вузов /
Т.С. Соболева, А.В. Чечкин; под ред. А.В. Чечкина. —
М.: Издательский центр «Академия», 2006. — С. 96 – 108. —
(Университетский учебник. Сер. Прикладная математика и информатика).

Горбатов В.А.Основы дискретной математики / Учеб. пособие для вузов. — М: Высшая школа, 1986. — 312 с.;

Горбатов В.А.Фундаментальные основы дискретной математики. Информационная математика: Учеб. пособие для вузов. — М.: Наука, 2000. — 540 с.;

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат, 1988 г. — 450 с.

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат, 1988 г. — 450 с.

Там же.

Горбатов В.А.Основы дискретной математики / Учеб. пособие для вузов. — М: Высшая школа, 1986. — 312 с.

Там же.

Там же.

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат, 1988 г. — 450 с.

Горбатов В.А.Основы дискретной математики / Учеб. пособие для вузов. — М: Высшая школа, 1986. — 312 с.

Там же.

Кузнецов О.П.Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. — М: Энергоатомиздат, 1988 г. — 450 с.

Там же.

Там же.

Там же.

Горбатов В.А.Основы дискретной математики / Учеб. пособие для вузов. — М: Высшая школа, 1986. — 312 с.

АЛГЕБРА ЛОГИКИ