Формулы алгебры логики

Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.

В качестве примеров высказываний приведем предложения «НГТУ — крупнейший вуз Новосибирска» и «Снег зеленый». Первое высказывание является истинным, а второе — ложным.

Поставим в соответствие высказыванию Р логическую переменную x , которая принимает значение 1, если Р истинно, и 0, если Р ложно.

Если имеется несколько высказываний, то из них можно образовать различные новые высказывания. При этом исходные высказывания называются простыми , а вновь образованные — сложными . Соответственно из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.

Итак, пусть {xi | i ∈ I } некоторое множество логических переменных. Определим по индукции понятие формулы алгебры логики :

1) любая логическая переменная является формулой (называемой атомарной );

2) если φ и ψ — формулы, то выражения φ, (φ ∧ ψ), (φ ∨ ψ), (φ → ψ), (φ ↔ ψ) являются формулами;

3) никаких других формул, кроме построенных по пп. 1 и 2, нет.

Если формула φ построена из логических переменных, лежащих в множестве {x 1, x 2, …, xn}, то будем писать φ(x 1, x 2, …, xn).

Символы , ∧ , ∨ , →, ↔, использованные в определении, называются логическими операциями или связками и читаются соотвественно: отрицание , конъюнкция , дизъюнкция , импликация и эквивалентность .

Введенные в п.2 формулы следующим образом интерпретируются в русском языке: φ — «не φ», (φ ∧ ψ) — «φ и ψ», (φ ∨ ψ) — «φ или ψ», (φ → ψ) — «если φ, то ψ», (φ ↔ ψ) — «φ тогда и только тогда, когда ψ».

Вместо φ часто пишут , вместо (φ ∧ ψ) — (φ & ψ), (φ · ψ) или (φψ).

Действия логических операций задаются таблицами истинности , каждой строке которых взаимно однозначно сопоставляется набор значений переменных, составляющих формулу, и соответствующее этому набору значение полученной формулы:

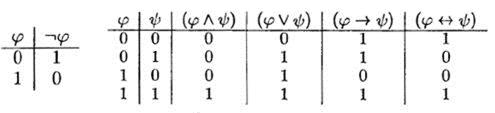
Приведенные таблицы истинности называются также интерпретациями логических операций и составляют семантику формул (т. е. придание смысла формулам) в отличие от синтаксиса формул (т. е. формальных законов их построения, данных в определении формулы).

Исходя из таблиц истинности для логических операций, можно строить таблицы истинности для произвольных формул.

Пример 1.1. Построить таблицу истинности для формулы

Будем строить таблицу истинности последовательно в соответствии с шагами построения формулы φ:

Легко заметить, что таблица истинности для φ совпадает с таблицей истинности для .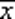

Расширим понятие формулы, введя новые, не менее важные логические операции:

— (φ| ψ) — штрих Шеффера или антиконъюнкция , по определению (φ| ψ) ⇌ (φ ∧ ψ);

— (φ↓ ψ) — стрелка Пирса или антидизъюнкция , по определению (φ↓ ψ) ⇌ (φ ∨ ψ);

— (φ⊕ ψ)) — кольцевая сумма , логическое сложение или сложение по модулю 2, по определению (φ⊕ ψ) ⇌ (φ ↔ ψ).

Составим, исходя из определений, таблицы истинности для этих трех операций:

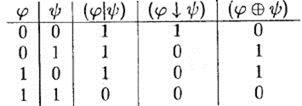
Как видно из примера 1.1, даже при составлении несложных формул возникает обилие скобок. Чтобы избежать этого, в алгебре логики, так же как и в арифметике, приняты некоторые соглашения относительно расстановки скобок. Перечислим эти соглашения.

1. Внешние скобки не пишутся. Например, вместо высказывания ((x ∨ y ) → z ) пишется (x ∨ y ) → z .

2. На множестве { , ∧ , ∨ , →, ↔, | , ↓ , ⊕ } вводится транзитивное отношение < «быть более сильным» и отношение эквивалентности ~ «быть равносильным» по правилам, показанным на рис. 6.1.

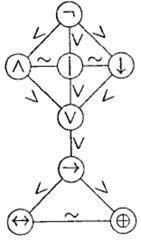
Рис. 6.1

Согласно этим отношениям недостающие скобки в формуле расставляются последовательно, начиная с наиболее сильных связок и кончая наиболее слабыми, а для равносильных связок расстановка скобок выполняется слева направо.