Эквивалентность формул

Формулы φ (x 1, x 2, …, xn) и ψ(x 1, x 2, …, xn) называются эквивалентными (φ ~ ψ), если совпадают их таблицы истинности, т. е. совпадают представляемые этими формулами функции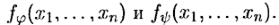

Отметим основные эквивалентности между формулами:

1) ((φ ∧ ψ) ∧ χ) ~ (φ ∧ (ψ ∧ χ)), ((φ ∨ ψ) ∨ χ) ~ (φ ∨ (ψ ∨ χ)) (ассоциативность ∧ и ∨ );

2) (φ ∧ ψ) ~ (φ ∧ ψ ), (φ ∨ ψ) ~ (φ ∨ ψ ) (коммутативность ∧ и ∨ );

3) (φ ∧ φ ) ~ φ , (φ ∨ φ ) ~ φ (идемпотентность ∧ и ∨ );

4) (φ ∧ (ψ ∨ χ)) ~ ((φ ∧ ψ) ∨ (φ ∧ χ)), (φ ∨ (ψ ∧ χ)) ~ ((φ ∨ ψ) ∧ (φ ∨ χ)) (законы дистрибутивности );

5) (φ ∧ (φ ∨ ψ) ~ φ , (φ ∨ (φ ∧ ψ) ~ φ (законы поглощения );

6) (φ ∧ ψ) ~ φ ∨ ψ, (φ ∨ ψ) ~ φ ∧ ψ (законы де Моргана )

7) φ ~ φ (закон двойного отрицания);

8) φ → ψ ~ φ ∨ ψ;

9) φ ↔ ψ ~ ((φ → ψ) ∧ (ψ → φ ) ~ ( φ ∨ ψ) ∧ ( ψ ∨ φ );

10) (φ ∨ φ ψ) ~ (φ ∨ ψ), ( φ ∨ φ ψ) ~ ( φ ∨ ψ);

11) φ ( φ ∨ ψ) ~ φ ψ, φ (φ ∨ ψ) ~ φ ψ

Формула φ (x 1, x 2, …, xn) называется выполнимой (опровержимой ), если существует такой набор значений переменных, при котором формула принимает значение 1 (соответственно 0).

Формула φ (x 1, x 2, …, xn) называется тождественно истинной общезначимой или тавтологией (тождественно ложной или противоречием ), если эта формула принимает значение 1 (соответственно 0) при всех наборах значений переменных, т. е. функция f является константой 1 (константой 0).

Если φ — тождественно истинная формула, то будем писать ⊨ φ . В противном случае пишем ⊭ φ .

Таким образом, ⊨ 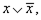⊭ x ∧ y , ⊭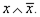

Формула φ тождественно ложна тогда и только тогда , когда φ тождественно истинна (⊨ φ );

Формула φ опровержима тогда и только тогда , когда она не является тождественно истинной (⊭ φ );

Формула φ выполнима тогда и только тогда , когда она не является тождественно ложной .

Отметим, что тождественно истинные (соответственно тождественно ложные) формулы образуют класс эквивалентности по отношению ~.