III. Методика измерений и расчетные формулы. Работа выполняется на установке ФМ-15, общий вид которой представлен на рис.1

ИЗУЧЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ ЭНЕРГИИ И МОМЕНТА ИМПУЛЬСА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

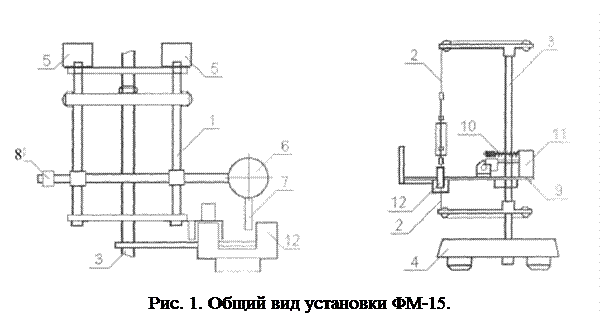
Работа выполняется на установке ФМ-15, общий вид которой представлен на рис.1. Основным элементом установки является крутильный маятник, представляющий собой металлическую рамку 1, подвешенную на стальной нити 2. Нить подвеса закреплена вертикально в натянутом состоянии на стойке 3 с основанием 4. Рамка может совершать крутильные колебания вокруг вертикальной оси, проходящей через ее ось симметрии. На ней имеются места для крепления двух дополнительных грузов 5 симметрично относительно оси. К ней же крепится «мишень» 6 в виде диска, поверхность которого покрыта тонким слоем пластилина, флажок 7 для контроля ее колебаний и противовес 8. «Пулей» служит металлическая втулка. К стойке на кронштейне 9 крепится «пистолет», состоящий из направляющего стержня с пружиной 10 и спускового устройства 11. К стойке также на кронштейне крепится фотодатчик 12. Регистрация числа и времени колебаний осуществляется блоком электронным ФМ-1/1 (на рис.1 не показан).

Если освободить пулю от стреляющего устройства, то она вклеится в пластилин на мишени крутильного маятника и вызовет отклонение последнего на некоторый угол от положения равновесия. Кинетическая энергия маятника, полученная им от пули, постепенно будет переходить в потенциальную энергию упругой деформации закручивающейся нити. Затем начнется процесс перехода потенциальной энергии в кинетическую и т.д. Маятник будет совершать гармонические крутильные колебания, период которых значительно больше времени соударения.

III. Методика измерений и расчетные формулы.

Систему пуля - маятник можно считать замкнутой. Применим к ней закон сохранения момента импульса:

,

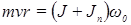где m и v — масса и скорость пули соответственно; r — расстояние от оси вращения маятника до центра масс пули в месте ее вклеивания; J — момент инерции маятника; J_п — момент инерции пули относительно оси вращения маятника; ω₀ — начальная угловая скорость маятника.

Поскольку J_п << J, то

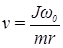. (1)

Из (1) следует, что для определения скорости пули необходимо найти момент инерции и начальную угловую скорость маятника; величины m и r могут быть измерены прямо.

Для определения ω₀ воспользуемся законом сохранения механической энергии и основным законом динамики вращательного движения.

Маятник совершает крутильные колебания под действием упругого момента нити, пропорционального углу поворота маятника φ:

,

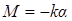где k — модуль кручения. Знак минус указывает на то, что псеводвектор М направлен против псевдовектора φ отклонения маятника.

Элементарная работа против сил упругости по закручиванию нити на малый угол dφ равна:

.

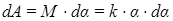После интегрирования получаем: .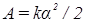

Если пренебречь незначительными потерями на трение, то можно записать:

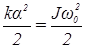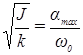, или , (2)

где α_max — максимальный угол отклонения маятника от положения равновесия.

По закону динамики вращательного движения:

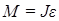, или .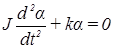

Частным решением этого уравнения является

,

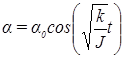в чем можно убедиться непосредственной подстановкой.

Величина 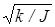в последнем выражении является циклической частотой колебаний, которая по определению равна 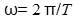.Таким образом, маятник будет совершать гармонические колебания с периодом

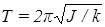. (3)

Подставив в формулу (3) выражение для 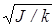из формулы (2), получим следующее выражение для начальной угловой скорости маятника:

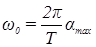. (4)

Для определения скорости пули требуется также найти момент инерции, для определения которого, в свою очередь, необходимо найти жесткость подвеса k. Величину k можно исключить, если измерить сначала период колебаний пустой рамки (T₀), а затем установить на рамку грузы 5 (см. рис. 1) и измерить период колебаний рамки с грузами (T₁). Решая совместно уравнения вида (3) для пустой и нагруженной рамки, получим момент инерции пустой рамки:

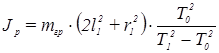, (5)

где m_гр — масса груза, r₁ — радиус груза, ℓ₁ — расстояние от оси вращения рамки до оси грузов.

Момент инерции нагруженной рамки составляет:

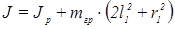. (6)