Минимизация булевых функций в классе ДНФ

Каждая формула имеет конечное число вхождений переменных. Под вхождением переменной понимается место, которое переменная занимает в формуле. Задача заключается в том, чтобы для данной булевой функции f найти ДНФ, представляющую эту функцию и имеющую наименьшее число вхождений переменных.

Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза.

Пример 6.1. Формула 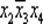— элементарное произведение, а формула 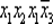элементарным произведением не является.

Формула φ(x 1, x 2, …, xn) называется импликантой формулы ψ(x 1, x 2, …, xn), если φ — элементарное произведение и φ ∧ ψ ~ φ , т. е. для соответствующих формулам φ и ψ функций 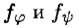справедливо неравенство 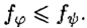Формула φ(x 1, x 2, …, xn) называется импликантой функции f , если φ — импликанта совершенной ДНФ, представляющей функцию f . Импликанта 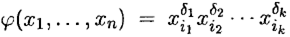формулы ψ называется простой , если после отбрасывания любой литеры из φ не получается формула, являющаяся импликантой формулы ψ.

Дизъюнкция всех простых импликант данной формулы (функции) называется сокращенной ДНФ .

Теорема 6.1. Любая булева функция , не являющаяся константой 0, представима в виде сокращенной ДНФ .

Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицы истинности. Если из сокращенной ДНФ удалить все лишние импликанты, то получается ДНФ, называемая тупиковой .

Заметим, что представление функции в виде тупиковой ДНФ в общем случае неоднозначно.

Выбор из всех тупиковых форм формы с наименьшим числом вхождений переменных дает минимальную ДНФ (МНДФ ).

Рассмотрим метод Квайна для нахождения МДНФ, представляющей данную булеву функцию. Определим следующие три операции:

— операция полного склеивания — ;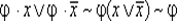

— операция неполного склеивания — ;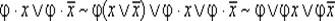

— операция элементарного поглощения — .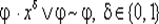

Теорема 6.2 (теорема Квайна). Если исходя из совершенной ДНФ функции произвести все возможные операции неполного склеивания , а затем элементарного поглощения , то в результате получится сокращенная ДНФ , т. е. дизъюнкция всех простых импликант .

В силу принципа двойственности для булевых алгебр все приведенные понятия и рассуждения очевидным образом можно преобразовать для нахождения минимальных конъюнктивных нормальных форм (МКНФ).

Карты Карно

Другой способ получения простых импликант формул с малым числом переменных (и, значит, нахождения с помощью матрицы Квайна минимальной ДНФ) основан на использовании так называемых карт Карно .

Карта Карно для п переменных служит эффективным средством иллюстративного представления n -куба. Она содержит 2nячеек, каждая из которых соответствует одной из 2nвозможных комбинаций значений п логических переменных x 1, x 2, …, xn. Карта строится в виде матрицы размера 2n – kна 2kтак, что ее столбцы соответствуют значениям переменных x 1, x 2, …, xk, строки — значениям переменных xk + 1 , … xn, а соседние ячейки (как по вертикали, так и по горизонтали) отличаются только значением одной переменной (рис. 6.5).

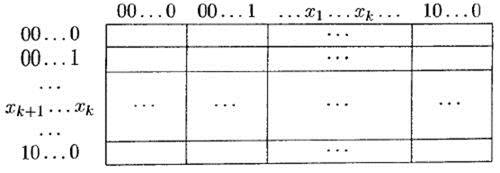
Рис. 6.5

На рис. 6.6 приведены карты Карно для функций трех и четырех переменных соответственно. В этих картах все ячейки, отмеченные скобкой xi(по строке и столбцу), представляют входные комбинации с xi= 1, а в неотмеченных строках и столбцах ячейки соответствуют комбинациям с xi= 0 (см. рис. 6.6a , на котором разными способами изображена одна и та же карта). Например, на рис. 6.6а ячейка а соответствует набору 001 значений переменных x 1, x 2, x 3. Отметим, что для каждой функции может быть построено несколько различных карт. На рис. 6.6б изображены две карты Карно для функции четырех переменных. Первая карта соответствует разбиению переменных {{x l, x 2}, {x 3, x 4}}, а вторая — {{х 1}, {х 2, х 3, х 4}}.

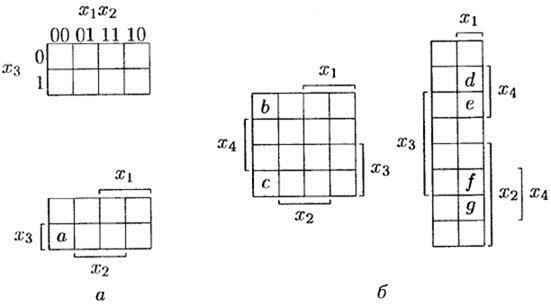
Рис. 6.6

У каждой вершины n -куба есть ровно п смежных с ней вершин, т. е. вершин, отличающихся от нее только одной координатой. Поскольку в карте Карно каждая ячейка может иметь не более четырех ячеек, соседних по строке или столбцу, для представления точек, отличающихся только на одну координату, необходимо использовать и более удаленные ячейки. Например, точки b и c на рис. 6.6б отличаются только значением переменной x 3, т. е. являются смежными.

Булева функция может быть представлена на карте Карно выделением 1-ячеек (т. е. ячеек, в которых функция принимает значение, равное 1). Подразумевается, что необозначенные ячейки соответствуют 0-точкам.

На рис. 6.7 изображена карта, представляющая булеву функцию f (x , y , z ), для которой f (0, 0, 0) = f (1, 1, 0) = f (1, 1, 1) = f (1, 0, 1) = 0, f (0, 1, 0) = f (1, 0, 0) = f (0, 0, 1) = f (0, 1, 1) = 1.

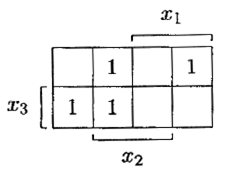
Рис. 6.7

Для построения импликант берутся всевозможные наборы 1-ячеек, образующих вершины некоторого k -куба (т. е. 2kточек таких, что пары соседних отличаются ровно одной координатой). Совпадающие координаты образуют набор (δ1, …, δn – k), и требуемая импликанта имеет вид 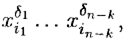— переменная, соответствующая значению δj.

Определение простых импликант функции сводится к нахождению всех k -кубов, которые не содержатся в кубах более высокого порядка.

После нахождения простых импликант задача построения минимальной ДНФ сводится к изучению матрицы Квайна. При наглядном размещении простых импликант в карте Карно удается непосредственно находить минимальную ДНФ, выбирая те простые импликанты, которые покрывают все единицы и имеют наименьшее возможное число вхождений переменных. Так, минимальной ДНФ для функции, изображенной на рис. 6.8, является формула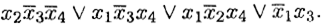

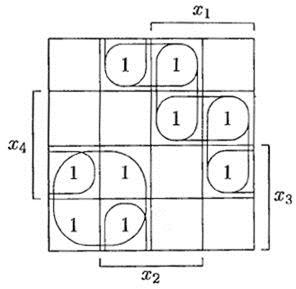
Рис. 6.8

Логические сети