Определение и реализация булевых функций

Мультиграф G = á M , U , R ñ , в котором выделено k вершин (полюсов ), называется k -полюсной сетью . Сеть G , задаваемая неориентированным мультиграфом с k полюсами, в которой каждое ребро помечено буквой из алфавита 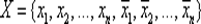, называется k -полюсной контактной схемой .

На рис. 6.21 приведен пример контактной схемы с двумя полюсами a 1и a 6.

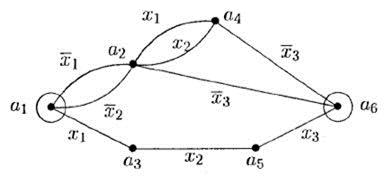
Рис. 6.21

(k + 1)-полюсная схема, в которой один полюс выделен (он называется входным ), а остальные полюса (выходные ) равноправны, называется (1, k )-полюсником . Таким образом, если в приведенной на рис. 6.21 двухполюсной схеме рассматривать, например, полюс a 1как входной, а полюс a 6как выходной, то получаем (1, 1)-полюсник .

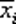Ребра контактной схемы называются контактами . Контакт, соответствующий логической переменной xi, называется замыкающим и обозначается через Замыкающий контакт пропускает ток при xi= 1. Контакт, соответствующий литере , называется размыкающим и обозначается как 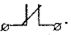Через него ток проходит при xi = 0. Таким образом, значение 1 интерпретируется как состояние переключателя «ток проходит», а 0 — «ток не проходит». Функции xi∧ xjсоответствует последовательное соединение контактов 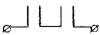, а функции xi∨ xj— параллельное соединение контактов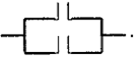

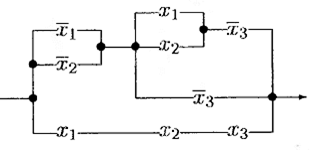
Рис. 6.22

Нетрудно заметить, что схеме, показанной на рис. 6.21, соответствует электрическая схема , приведенная на рис. 6.22, а также схема контактов , изображенная на рис. 6.23. На последнем рисунке показаны контакты, зависящие от значений переменных x 1, x 2, x 3, а также схема соединений контактов.

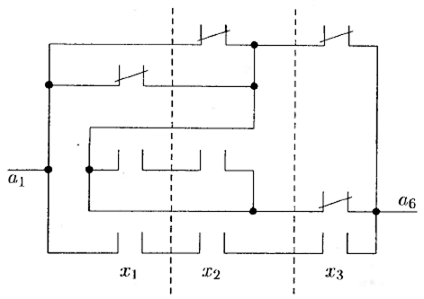
Рис. 6.23

Пусть a , b — полюса контактной схемы ∑, [a , b ] — некоторая цепь из а в b , K [a, b]— конъюнкция литер, приписанных ребрам цепи [a , b ]. Функция fa,b(X ), определяемая формулой 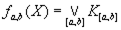, в которой дизъюнкция берется по всем простым цепям схемы, соединяющим полюса а и b , называется функцией проводимости между полюсами а и b схемы ∑.

Говорят, что функция g (Х ) реализуется (1, k )-полюсником , если существует такой выходной полюс bi, что fa,b(X ) = g (Х ), где а — входной полюс. (1, 1)-полюсники называются эквивалентными , если они реализуют одну и ту же булеву функцию. Сложностью (1, 1)-полюсника называется число контактов. (1, 1)-полюсник, имеющий наименьшую сложность среди эквивалентных ему схем, называется минимальным . Сложность минимального (1, 1)-полюсника, реализующего функцию f называется сложностью функции f в классе (1, 1)-полюсников и обозначается через L π(f ).

Заметим, что задача нахождения минимального (1, 1)-полюсника среди эквивалентных данному (1, 1)-полюснику ∑ равносильна нахождению среди функций, реализуемых схемой ∑, функции, имеющей наименьшее число вхождений переменных. Действительно, функцию, реализуемую (1, 1)-полюсником, нетрудно представить в виде формулы, которая строится из литер в соответствии с контактной схемой и имеет ровно столько вхождений переменных, сколько контактов имеет схема. Например, изображенной па рис. 6 .23 схеме соответствует булева функция

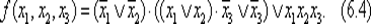
Таким образом, задача нахождения минимального (1, 1)-полюсника сводится к минимизации соответствующей булевой функции.

Эффективное уменьшение числа контактов достигается с помощью нахождения минимальной ДНФ булевой функции.

Найдем минимальную ДНФ функции (6.4), реализуемой схемой рис. 6.22. Придавая логическим переменным x 1, x 2, x 3всевозможные значения, по схеме или формуле (6.4) получаем таблицу истинности:

по которой определим совершенную ДНФ: 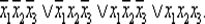Используя один из методов нахождения минимальной ДНФ. получаем формулу 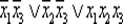, эквивалентную формуле (6.4) и соответствующую схеме, состоящей из семи контактов (рис. 6.24а).

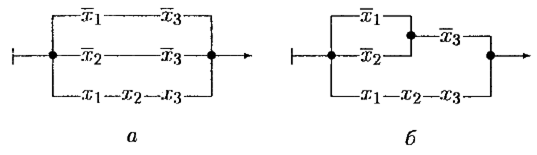
Рис. 6.24

Отметим, что схема, изображенная на рис. 6.24а, допускает упрощение, соответствующее формуле 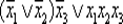, которое приведено на рис. 6.24б и является минимальной схемой. Сложность минимальной схемы равна 6: L π(f ) = 6.